Motivation for consistent hashing:

• Minimize keys that needs to be re-distributed when servers are added or removed
• Easy to scale horizontally - wants data to be more evenly distributed

REF: https://www.slideshare.net/oemebamo/introduction-to-memcached and https://serhatgiydiren.github.io/system-design-interview-distributed-cache

Caching

• A copy of real data with faster(and/or cheaper) access

Simple Key/Value Store with the following operations save, get and delete.

Functional Requirements

• put(key, value) : Stores object in the cache under some unique key
• get(key) : Retrieves object from the cache based on the key

Non-Functional Requirements

• Scalable (scales out easily together with increasing number of requests and data) : High scalability will help to ensure our cache can handle increased number of put and get requests. And be able to handle increasing amount of data we may need to store in the cache.
• Highly Available (tolerates hardware / network failures, no single point of failure)
• Highly Performant (fast put / get)

Terminology

• Storage cost
• Retrieval cost (network load/algorithm load)
• Invalidation(Keeping data up to date/removing irrelevant data)
• Replacement policy(FIFO, LRU, LFU, MRU, Random vs Beladys algorithm)

• Cold cache/ Warm cache

• Cache hit and cache miss
  • hit_ratio (hits / hits + misses)
  • miss ratio ( 1 - hit_ratio)
  • Cache are only efficient when benefits of faster access outweight overhead of checking and maintaining cache(keeping cache up to date) => More cache hits then cache misses

Cache access patterns:

• Write through: whenever any “write” request comes, it will come through the cache to the DB. Write is considered successful only iff data is written successfully in the cache and in DB.
• Write around: Write request goes around the cache straight to DB and acknowledge is sent back, data is not sent to cache. Data is written to the cache when there is the first cache miss.
• Write back: Write update goes to cache, data is saved in the cache, and acknowledge is send immediately. and then there is one more service that will sink the data to DB. Or say while replacing this entry, we can write to the db.

Working with HashTable:

• Given a key, we can find the hash function and take modulo to find the bucket/slot in which we have to put this entry. If there are collisions, we can resolve it with separate chaining, open addressing, robin hood hashing.

Collision Resolution Techniques

• Separate chaining technique creates a linked list to the slot for which collision occurs. Rehash data when the load factor(Number of elements/size of hash table) is too high.
• Open Addressing: Unlike separate chaining, all the keys are stored inside the hash table. Probing is performed until an empty bucket is found. Once an empty bucket is found, the key is inserted.
  • Linear Probing: When collision occurs, we linearly probe for the next bucket until an empty bucket is found.
  • Quadratic Probing: Quadratic probing operates by taking the original hash index and adding successive values of an arbitrary quadratic polynomial until an open slot is found. Example sequence: H+1^2, H+2^2, H+3^2, H+4^2,…, H+k^2
  • Double hashing: We use another hash function hash2(x) and look for i * hash2(x) bucket in ith iteration.
  • Deletion is difficult in open addressing, will need to rearrange few keys after deletion, may be we will need to use dead flag(we can insert new elements in this slot).

The problem of naive hashing function

A naive hashing function is key % n where n is the number of servers.

It has two major drawbacks:

• NOT horizontally scalable, or in other words, NOT partition tolerant. When you add new servers, all existing mapping are broken. It could introduce painful maintenance work and downtime to the system.
• May NOT be load balanced. If the data is not uniformly distributed, this might cause some servers to be hot and saturated while others idle and almost empty.

Problem 2 can be resolved by hashing the key first, hash(key) % n, so that the hashed keys will be likely to be distributed more evenly. But this can’t solve the problem 1. We need to find a solution that can distribute the keys and is not dependent on n.

Scaling Out: Distributed Hashing

REF: https://www.toptal.com/big-data/consistent-hashing and https://medium.com/omarelgabrys-blog/consistent-hashing-beyond-the-basics-525304a12ba and http://www.ines-panker.com/2019/07/29/consistent-hashing.html

In some situations, it may be necessary or desirable to split a hash table into several parts, hosted by different servers. One of the main motivations for this is to bypass the memory limitations of using a single computer, allowing for the construction of arbitrarily large hash tables (given enough servers).

• The simplest way is to take the hash modulo of the number of servers. That is, server = hash(key) mod N, where N is the size of the pool.
• To store or retrieve a key, the client first computes the hash, applies a modulo N operation, and uses the resulting index to contact the appropriate server (probably by using a lookup table of IP addresses).

Note that the hash function used for key distribution must be the same one across all clients, but it need not be the same one used internally by the caching servers.

The Rehashing Problem

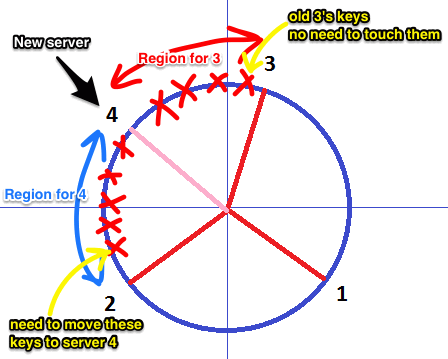
This distribution scheme is simple, intuitive, and works fine. That is, until the number of servers changes.

What happens if one of the servers crashes or becomes unavailable? Keys need to be redistributed to account for the missing server, of course. The same applies if one or more new servers are added to the pool;keys need to be redistributed to include the new servers. This is true for any distribution scheme, but the problem with our simple modulo distribution is that when the number of servers changes, most hashes modulo N will change, so most keys will need to be moved to a different server.

So, even if a single server is removed or added, all keys will likely need to be rehashed into a different server.

Solution: Consistent Hashing

Consistent Hashing is a distributed hashing scheme that operates independently of the number of servers or objects in a distributed hash table by assigning them a position on an abstract circle, or hash ring. This allows servers and objects to scale without affecting the overall system.

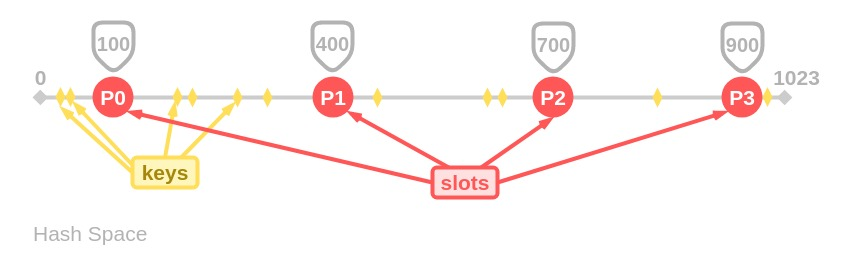
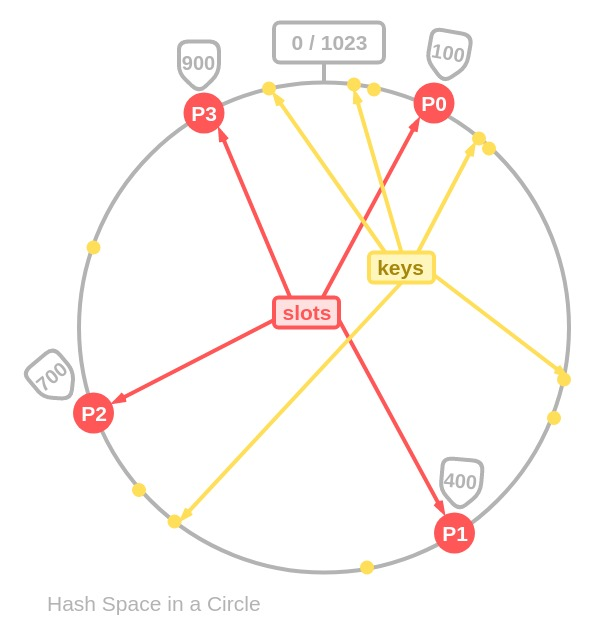
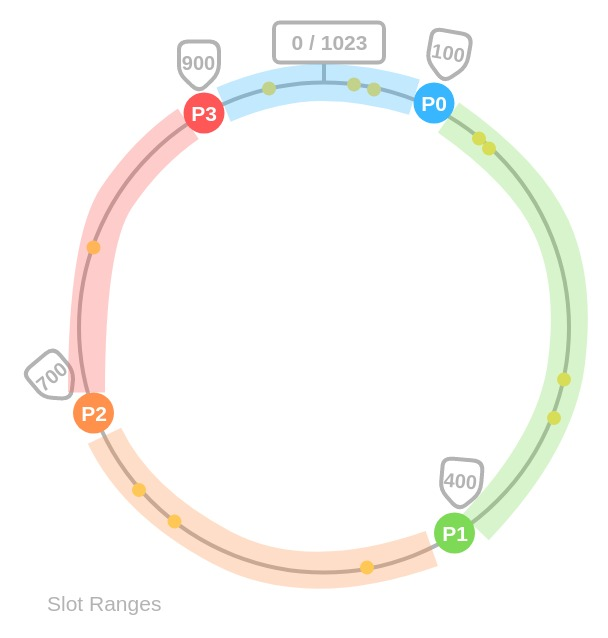
Since we have the keys for both the objects and the servers on the same circle, we may define a simple rule to associate the former with the latter: Each object key will belong in the server whose key is closest, in a counterclockwise direction(or clockwise, depending on the conventions used).

There are clients for several systems, such as Memcached and Redis, that include support for consistent hashing out of the box.

Issues with Basic approach of Consistent hashing

• It is impossible to keep the same size of partitions on the ring for all servers considering a server can be added or removed. A partition is the hash space betweeen adjacent servers. It is possible that size of the partitions on the ring assigned to each server is very small or fairly large.
• It is possible to have a non-uniform key distribution on the ring. This might lead to hotspots because few servers will be accessed many more times than others.

A technique called virtual nodes or replicas is used to solve these problems.

A virtual node refers to the real node, each server is represented by multiple virtual nodes on the ring. For example if we assume each server has 3 virtual nodes(in real-world systems, the number of virtual nodes is much larger), server A will be mapped to A0, A1 and A2. Instead of just A, we can have A0, A1 and A2 to represent server A on the ring.

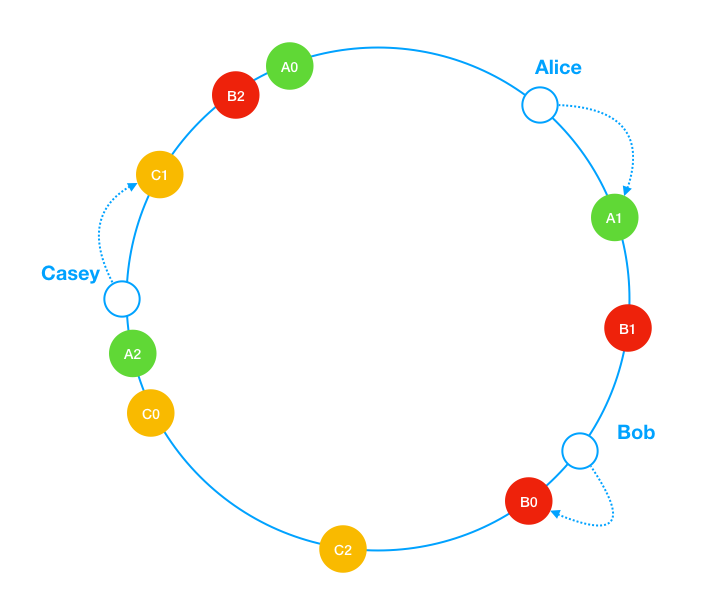
Ref: https://liuzhenglaichn.gitbook.io/system-design/advanced/consistent-hashing