Notes

Suppose we have an array A and we want to support the following two operations:

• Update: change the value of an element A_i
• Query: find the value of a certain partial sum A_1 + A_2 + ... + A_i

Note

The Binary Indexed Tree, as presented by Peter Fenwick, cannot efficiently answer min/max kinds of queries, because, for determining the sum of A[i ... j], it needs to compute the difference between the sum of the first j elements and the sum of the first i – 1 elements.

// Binary indexed tree supporting binary search.
struct BIT {
    int n;
    vector<int> bit;
    // BIT can be thought of as having entries f[1], ..., f[n]
    // with f[1]=0,...,f[n]=0 initially
    BIT(int n):n(n), bit(n+1) {}
    // returns f[1] + ... + f[idx-1]
    // precondition idx <= n+1
    int read(int idx) {
        idx--;
        int res = 0;
        while (idx > 0) {
            res += bit[idx];
            idx -= idx & -idx;
        }
        return res;
    }
    // returns f[idx1] + ... + f[idx2-1]
    // precondition idx1 <= idx2 <= n+1
    int read2(int idx1, int idx2) {
        return read(idx2) - read(idx1);
    }
    // adds val to f[idx]
    // precondition 1 <= idx <= n (there is no element 0!)
    void update(int idx, int val) {
        while (idx <= n) {
            bit[idx] += val;
            idx += idx & -idx;
        }
    }
    // returns smallest positive idx such that read(idx) >= target
    int lower_bound(int target) {
        if (target <= 0) return 1;
        int pwr = 1; while (2*pwr <= n) pwr*=2;
        int idx = 0; int tot = 0;
        for (; pwr; pwr >>= 1) {
            if (idx+pwr > n) continue;
            if (tot + bit[idx+pwr] < target) {
                tot += bit[idx+=pwr];
            }
        }
	// here it is read(idx) >= target
	// hence when querying directly use idx + 1 in code
	// or use lower_bound(target) - 1
        return idx+2;
    }
    // returns smallest positive idx such that read(idx) > target
    int upper_bound(int target) {
        if (target < 0) return 1;
        int pwr = 1; while (2*pwr <= n) pwr*=2;
        int idx = 0; int tot = 0;
        for (; pwr; pwr >>= 1) {
            if (idx+pwr > n) continue;
            if (tot + bit[idx+pwr] <= target) {
                tot += bit[idx+=pwr];
            }
        }
        return idx+2;
    }
};

lower_bound can be used as an ordered set/multiset on indices by using the tree as a 0/1 or frequency array

Idea:

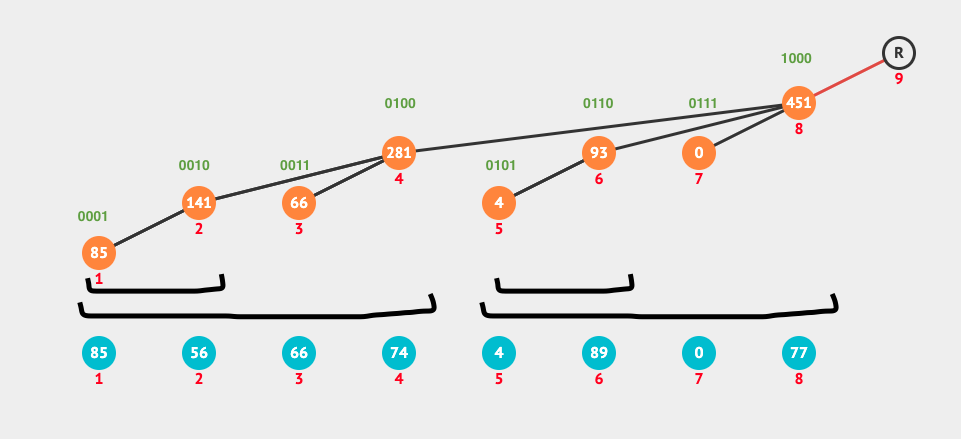
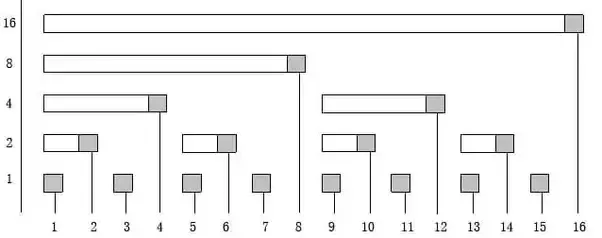
• Let idx be an index of BIT. Let r be the position in idx of its last non-zero digit in binary notation, i.e., r is the position of the least significant non-zero bit of idx.
• bit[idx] holds the sum of frequencies for indices (idx - 2^r + 1) through idx, inclusive

source: https://github.com/t3nsor/codebook/blob/master/BIT.cpp

Explanation

A Fenwick tree or a binary indexed tree is a data structure that handles both of these efficiently. It should be noted that if we have such a data structure, we can also find the sum over an interval [i, j] by just calculating sum(j) - sum(i-1).

To represent a negative value −x, we take the binary representation of x, complement it, and then add 1 (ignoring the final carry). Let's take an example where the numbers are represented on 8 bits for simplicity:

 x = 01101100
~x = 10010011
-x = 10010100 

Notice the bits more significant than the lsb are different for x and −x, while the lsb and the following 0's are the same. Therefore, x & -x gives the wanted answer, in our case:

Now we have a method of finding the length of any interval in O(1):

int lsb(int pos) {
    return pos & -pos;
}

#define LSOne(S) (S&(-S)) is used to get the last set bit of S

Update

void update(int pos, int val) {
    while (pos <= N) {
        fenwick[pos] += val;
        pos += lsb(pos);
    }
}

Query

int query(int pos) {
   int sum = 0;
   while (pos > 0) {
      sum += fenwick[pos];
      pos -= lsb(pos);
   }
   return sum;
}

source: https://csacademy.com/lesson/fenwick_trees/

Struct based implementation

template < typename T >
struct binary_indexed_tree {
    int N;
    vector<T> BIT;
    binary_indexed_tree(int N): N(N), BIT(N + 1, 0) {}
    void add(int i, T x) {
        i++; // incremented internal index i
        while (i <= N) {
            BIT[i] += x;
            i += i & -i;
        }
    }
    T sum(int i) {
        T ans = 0;
        while (i > 0) {
            ans += BIT[i];
            i -= i & -i;
        }
        return ans;
    }
    // finds sum from [L, R)
    T sum(int L, int R) {
        return sum(R) - sum(L);
    }
};

// Usage: 
// struct binary_indexed_tree<int> bit(2* 1e4 + 10);
// bit.add(i, 1);


// Use zero based indexing while updating etc
// struct binary_indexed_tree<int> *bit;
// bit = new binary_indexed_tree<int>(3* 1e4 + 10);
// bit->add(i, nums[i]); // i is zero based index
// bit->sum(left, right+1); // sum from [left, right]

source: https://codeforces.com/contest/1535/submission/118419611

template<typename T>
struct fenwick_tree {
    int tree_n = 0;
    T tree_sum = 0;
    vector<T> tree;
 
    fenwick_tree(int n = -1) {
        if (n >= 0)
            init(n);
    }
 
    void init(int n) {
        tree_n = n;
        tree_sum = 0;
        tree.assign(tree_n + 1, 0);
    }
 
    // O(n) initialization of the Fenwick tree.
    template<typename T_array>
    void build(const T_array &initial) {
        assert(int(initial.size()) == tree_n);
        tree_sum = 0;
 
        for (int i = 1; i <= tree_n; i++) {
            tree[i] = initial[i - 1];
            tree_sum += initial[i - 1];
 
            for (int k = (i & -i) >> 1; k > 0; k >>= 1)
                tree[i] += tree[i - k];
        }
    }
 
    // index is in [0, tree_n).
    void update(int index, const T &change) {
        assert(0 <= index && index < tree_n);
        tree_sum += change;
 
        for (int i = index + 1; i <= tree_n; i += i & -i)
            tree[i] += change;
    }
 
    // Returns the sum of the range [0, count).
    T query(int count) const {
        assert(count <= tree_n);
        T sum = 0;
 
        for (int i = count; i > 0; i -= i & -i)
            sum += tree[i];
 
        return sum;
    }
 
    // Returns the sum of the range [start, tree_n).
    T query_suffix(int start) const {
        return tree_sum - query(start);
    }
 
    // Returns the sum of the range [a, b).
    T query(int a, int b) const {
        return query(b) - query(a);
    }
 
    // Returns the element at index a in O(1) amortized across every index. Equivalent to query(a, a + 1).
    T get(int a) const {
        assert(0 <= a && a < tree_n);
        int above = a + 1;
        T sum = tree[above];
        above -= above & -above;
 
        while (a != above) {
            sum -= tree[a];
            a -= a & -a;
        }
 
        return sum;
    }
 
    bool set(int index, T value) {
        assert(0 <= index && index < tree_n);
        T current = get(index);
 
        if (current == value)
            return false;
 
        update(index, value - current);
        return true;
    }
 
    // Returns the largest p in `[0, tree_n]` such that `query(p) <= sum`. Returns -1 if no such p exists (`sum < 0`).
    // Can be used as an ordered set/multiset on indices in `[0, tree_n)` by using the tree as a 0/1 or frequency array:
    // `set(index, 1)` is equivalent to insert(index). `update(index, +1)` is equivalent to multiset.insert(index).
    // `set(index, 0)` or `update(index, -1)` are equivalent to erase(index).
    // `get(index)` provides whether index is present or not, or the count of index (if multiset).
    // `query(index)` provides the count of elements < index.
    // `find_last_prefix(k)` finds the k-th smallest element (0-indexed). Returns `tree_n` for `sum >= set.size()`.
    int find_last_prefix(T sum) const {
        if (sum < 0)
            return -1;
 
        int prefix = 0;
 
        for (int k = 31 - __builtin_clz(tree_n); k >= 0; k--)
            if (prefix + (1 << k) <= tree_n && tree[prefix + (1 << k)] <= sum) {
                prefix += 1 << k;
                sum -= tree[prefix];
            }
 
        return prefix;
    }
};

source: neal https://codeforces.com/contest/1354/submission/80534648

The inversion number of a sequence A = [ a0, a1, a2, … , aN − 1 ] is the number of pairs of indices (i ,j) such that i < j and ai > aj.

The inversion number can be calculated in an O(NlogN) with a method like Fenwick Tree by adding 1 in place of ai and for aj, counting till n-sum(aj)

Benq's implementation

BIT

Generally BIT/Fenwick tree uses 1-based indexing. But here data is stored in 0..n-1 instead of the usual 1..n, hence whenever we want to access data[i], the code uses data[i-1].

add(p, val) is nothing but adding on 0-based indexing a[p] += val, the code first increments p(1-based indexing).

• sum(r) = a[0] + a[1] + ... + a[r-1]
• sum(l, r) = a[l] + a[l+1] + ... + a[r] - Becareful when you are querying for sum of n elements. It is sum(0, n-1)

In case you want to print data for debugging, use debug() << imie(range(tree.data.begin(), tree.data.begin()+n));

template<class T> struct BIT {
    int n; vector<T> data;
    void init(int _n) { n = _n; data.resize(n); }
    void add(int p, T x) { for (++p;p<=n;p+=p&-p) data[p-1] += x; }
    T sum(int l, int r) { return sum(r+1)-sum(l); }
    T sum(int r) { T s = 0; for(;r;r-=r&-r) s+=data[r-1]; return s; }
    int lower_bound(T sum) {
        if (sum <= 0) return -1;
        int pos = 0;
        for (int pw = 1<<25; pw; pw >>= 1) {
            int npos = pos+pw;
            if (npos <= n && data[npos-1] < sum)
                pos = npos, sum -= data[pos-1];
        }
        return pos;
    }
};

source: https://github.com/kth-competitive-programming/kactl/blob/main/content/data-structures/FenwickTree.h and https://github.com/bqi343/USACO/blob/master/Implementations/content/data-structures/1D%20Range%20Queries%20(9.2)/BIT.h

BIT Offline with Coordinate compression

typedef vector<int> vi;

#define all(x) begin(x), end(x)
#define sz(x) (int)x.size()
#define rsz resize
#define ub upper_bound
#define pb push_back

/**
 * Description: Offline BIT with coordinate compression. First do all 
   * updates with $\texttt{mode=0}$ and then call $\texttt{init()}$.
 * Source: Own
 * Verification: https://codeforces.com/contest/1361/problem/F
 */

template<class T> struct BIToff {
	bool mode = 0; vi v; vector<T> d;
	int atMost(int x) { return ub(all(v),x)-begin(v); } // how many <= x
	void upd(int x, T y) {
		if (!mode) { v.pb(x); return; }
		int p = atMost(x); assert(p && v[p-1] == x);
		for (;p<=sz(v);p+=p&-p) d[p] += y;
	}	
	void init() { assert(!mode); mode = 1;
		sort(all(v)); v.erase(unique(all(v)),end(v)); d.rsz(sz(v)+1); }
	T sum(int x) { assert(mode);
		T ans = 0; for (int p=atMost(x);p;p-=p&-p) ans += d[p];
		return ans; }
	T query(int x, int y) { return sum(y)-sum(x-1);}
};

source: https://github.com/bqi343/USACO/blob/master/Implementations/content/data-structures/1D%20Range%20Queries%20(9.2)/BIToff.h and https://codeforces.com/contest/1361/submission/82571701

BIT with range updates

Basically, for a BIT, there are two modes available:

1. Range query and point update (a)
2. Range update and point querying (b)

You are probably more familiar with BITs using (a).

For (b), it's just a very simple modification, so I'll try to explain it the best I can.

For (a), when you call update(x, v), it will add the value of v to the position at x, and calling query(x) will add up all the elements x' ≤ x and return that.

Now, to extend it to (b), we see that when we call update(x, v), it will affect all the queries x' ≥ x.

Therefore, to update a range [a, b], we can call update(a, v) and update(b+1, -v).

Then, to get a point, we call query(p). Note that this will actually return the actual value at p, not the cumulative sum.

Now, to see why this works, see the following examples.

Suppose we just called update(a,v) and update(b+1,-v).

Now, let's say we called query(p). We have three cases:

• p < a. p will not be affected by the updates, so query(p) will not be affected and still return the correct result
• p > b. p will be affected by the update(a,v) since p >= a, and update(b+1,-v) since p >= b+1, therefore, v-v=0 so everything cancels out and query(p) will not be affected and return the correct result
• a ≤ p ≤ b. p is only affected by update(a,v), but not update(b+1,-v), therefore, query(p)'s value is increased by v, and will return the correct result

CSES Problem Range Update Queries

https://cses.fi/problemset/task/1651/

const int nax = 2e5 + 10;

template<class T> struct BIT {
    int n; vector<T> data;
    void init(int _n) { n = _n; data.resize(n); }
    void add(int p, T x) { for (++p;p<=n;p+=p&-p) data[p-1] += x; }
    T sum(int l, int r) { return sum(r+1)-sum(l); }
    T sum(int r) { T s = 0; for(;r;r-=r&-r) s+=data[r-1]; return s; }
    int lower_bound(T sum) {
        if (sum <= 0) return -1;
        int pos = 0;
        for (int pw = 1<<25; pw; pw >>= 1) {
            int npos = pos+pw;
            if (npos <= n && data[npos-1] < sum)
                pos = npos, sum -= data[pos-1];
        }
        return pos;
    }
};

BIT<long long> tree;

int main() {
    tree.init(nax);
    int n, q; scanf("%d %d", &n, &q);
    vector<long long> V(n);
    for(int i=0;i<n;i++) scanf("%lld", &V[i]);
    while(q--){
        int type; scanf("%d", &type);
        if(type == 1){
            int a, b, u; scanf("%d %d %d", &a, &b, &u);
            tree.add(a-1, u);
            tree.add(b, -u);
        } else {
            int k; scanf("%d", &k);
            printf("%lld\n", V[k-1] + tree.sum(k));
        }
    }
    return 0;
}

3. Range update and range querying (c)

Similar to Range Update - Point query, we maintain a BIT (say B1)

• Add v to [a..b] --> Update(a,v) and Update(b+1,-v) on the BIT B1
• Query(p) on B1 now gives the correct value of A[p]

The answer we want is ( Sum(0..b) - Sum(0..a-1) ), so let's design Sum(0..p). The thing with BIT is, if you design it to work for one update ( which is easy to imagine ) and all possible queries on that one update, mostly it should work for multiple updates ;)

Lets consider just one update : Add v to [a..b], rest all are 0

Now, consider Sum(0..p) for all possible p

1. 0 ≤ p < a : 0
2. a ≤ p ≤ b : v * ( p - (a-1) )
3. b < p < n : v * ( b - (a-1) )

This suggests that, for a index p, if we have (v * p) we can get the Sum(0..p) by subtracting X from it

1. 0 ≤ p < a : slope = 0 and intercept = 0
2. a ≤ p ≤ b : slope = v and intercept = -v*(a-1)
3. b < p < n : slope = 0 and intercept = v*b - v*(a-1)

So, we need to maintain something else too, to get that extra intercept term and that should give 0 for p < a, -v*(a-1) for p in [a..b], v*b-v(a-1) for p > b.

Does this ring something ;) ? hoho ! one more BIT for keeping this intercept.

We need to maintain another BIT (say B2)

• Add v to [a..b] --> Update(a,-v*(a-1)) and Update(b+1,v*b) on the BIT B2
• Query(p) on B2 now gives the extra sum that should be subtracted from A[p]*p

In other words, we implement a Fenwick tree with range updates via a normal (point-update) Fenwick tree that stores linear functions instead of just values.

source: https://petr-mitrichev.blogspot.com/2013/05/fenwick-tree-range-updates.html

// BIT with range updates, inspired by Petr Mitrichev
struct BIT {
    int n;
    vector<int> slope;
    vector<int> intercept;
    // BIT can be thought of as having entries f[1], ..., f[n]
    // which are 0-initialized
    BIT(int n): n(n), slope(n+1), intercept(n+1) {}
    // returns f[1] + ... + f[idx-1]
    // precondition idx <= n+1
    int query(int idx) {
        int m = 0, b = 0;
        for (int i = idx-1; i > 0; i -= i&-i) {
            m += slope[i];
            b += intercept[i];
        }
        return m*idx + b;
    }
    // adds amt to f[i] for i in [idx1, idx2)
    // precondition 1 <= idx1 <= idx2 <= n+1 (you can't update element 0)
    void update(int idx1, int idx2, int amt) {
        for (int i = idx1; i <= n; i += i&-i) {
            slope[i] += amt;
            intercept[i] -= idx1*amt;
        }
        for (int i = idx2; i <= n; i += i&-i) {
            slope[i] -= amt;
            intercept[i] += idx2*amt;
        }
    }
};

source: https://github.com/t3nsor/codebook/blob/master/BIT-range.cpp

Persistent BIT

// BIT or Fenwick Tree
int n;
int tree[100005];
#define lowbit(x) x&(-x)

inline void modify(int x,int d){
	for(;x<=n;x+=lowbit(x))tree[x]+=d;
}

inline int query(int x){
	int ans=0;
	for(;x;x-=lowbit(x))ans+=tree[x];
	return ans;
}

Persistent Fenwick Tree using Fat Node persistence

#include<vector>
#include<algorithm>
#define lowbit(x) x&(-x)

struct P{
	int data,id;
	P(int d=0,int i=0):data(d),id(i){}
	inline friend bool operator<(const P &a,const P &b){
		return a.id<b.id;
	}
};

int n,now;
std::vector<P >tree[100005];

inline void init(){
	now=0;
	for(int i=1;i<=n;++i)tree[i].clear(),tree[i].push_back(P());
}

inline void modify(int x,int d){
	for(;x<=n;x+=lowbit(x))tree[x].push_back(P(tree[x].back().data+d,now));
	++now;
}

// Query the interval sum of the id operation, id is calculated from 0
inline int query(int x,int id){
	int ans=0;
	std::vector<P >::iterator a;
	for(;x;x-=lowbit(x)){
		a=std::upper_bound(tree[x].begin(),tree[x].end(),P(0,id))-1;
		ans+=a->data;
	}
	return ans;
}

TODO: https://www.cnblogs.com/RabbitHu/p/BIT.html and https://robert1003.github.io/2020/01/27/fenwick-tree.html