Notes
Fibonacci
Leonardo Fibonacci’s numbers are defined as fib(0) = 0, fib(1) = 1, and for n ≥ 2, fib(n) = fib(n − 1) + fib(n − 2).
Fibonacci numbers have many interesting properties. One of them is the Zeckendorf ’s theorem: Every positive integer can be written in a unique way as a sum of one or more distinct Fibonacci numbers such that the sum does not include any two consecutive Fibonacci numbers. For any given positive integer, a representation that satisfies Zeckendorf’s theorem can be found by using a Greedy algorithm: Choose the largest possible Fibonacci number at each step. For example: 100 = 89 + 8 + 3; 77 = 55 + 21 + 1, 18 = 13 + 5, etc.
Another property is the Pisano Period where the last one/last two/last three/last four digit(s) of a Fibonacci number repeats with a period of 60/300/1500/15000, respectively.
Linear Homogeneous Recurrence Relations
Theorem: Let c1 and c2 be real numbers. Suppose that r2 − c1r − c2 = 0 has two distinct roots r1 and r2. Then the sequence {an} is a solution of the recurrence relation an = c1an-1 + c2an-2 if and only if an = α1r1 n + α2r2n for n = 0, 1, 2,..., where α1 and α2 are constants.
Proof: Distinct roots are required because, say a0 = C0 and a1 = C1, then
a0 = C0 = α1 + α2 and a1 = C1 = α1r1 + α2r2 which implies that α1 = (C1 - C0r2)/(r1 - r2), this requires that r1 and r2 are different.
Above theorem does not apply when there is one characteristic root of multiplicity two. If this happens, then an = nr0n is another solution of the recurrence relation when r0 is a root of multiplicity two of the characteristic equation.
Binet's formula
F(n+2) = F(n+1) + F(n)
If we try to find a geomtric sequences with F(n) = kn, then
kn+2 = kn+1 + kn
k2 = k + 1
which implies
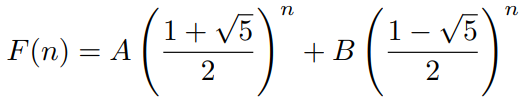
If we plug in two different values of n = 0 and n =1, and solve for A and B, we get:
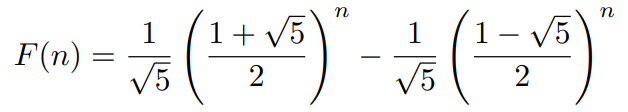
((1 + √5)/2) ≈ 1.618 Golden ratio
Fibonacci number system
https://www.johndcook.com/blog/2015/05/17/fibonacci-number-system/