Notes

Centroid Decomposition

Problem & Motivation

Given a tree, we are asked to find all the number of pairs (u, v) such that dist(u, v) ≤ D.

Solution

Note: This problem can also be solved by Small-To-Large Merging https://usaco.guide/plat/merging?lang=cpp

Let us fix one node of Tree by picking a vertex of the tree and call it c. Now let us split all the possible paths into classes:

1. Some of the paths may not include this vertex c, then it will be completely inside one of the subtrees formed after removing c.
2. If the path includes node c, then we can break into two segments u to c and c to v.

So what will do is that: We will pick a vertex c, remove that vertex from the tree and recursively find the number of pairs (u, v) in the subtree. In the end we will calculate the number of pairs which include the vertex c.

We will need to calculate d[v] which is distance from (c, v), this can be precalculated in linear time. If we fix vertex u, then we will need to find all the vertices such that d[v] ≤ D - d[u]. Say we have an array of distances d[i] and maintain sorted order of this array and find the number of nodes v using binary search.

In this problem we will need to find the vertices which belong to different subtrees. We can do it in the following ways:

1. Add elements of first subtree into binary search tree form left to right and then iterate for elements v of second subtree and query the number of elements u satisfying dist(u, v) ≤ D.
   Then add the elements of second subtree to binary search tree and continue. Each time we consider a subtree, all the elements of previous subtrees are in our binary search tree.

2. Another way to calculate is to subtract the values we don't want to include. For a node u calculate all the nodes v of tree such that d[v] ≤ D - d[u] and then subtract the number of nodes which are in the same subtree as u.

Important thing is how to choose node c. Time complexity depends on how good is the node c, when we use divide and conquer technique we want to divide our problem into subproblems of equal size. We choose our vertex to be centroid of the tree.

A centroid is defined as a vertex such that when removed, all of the resulting subtrees have a size of at most half that of the original tree (that is, ⌊n/2⌋).

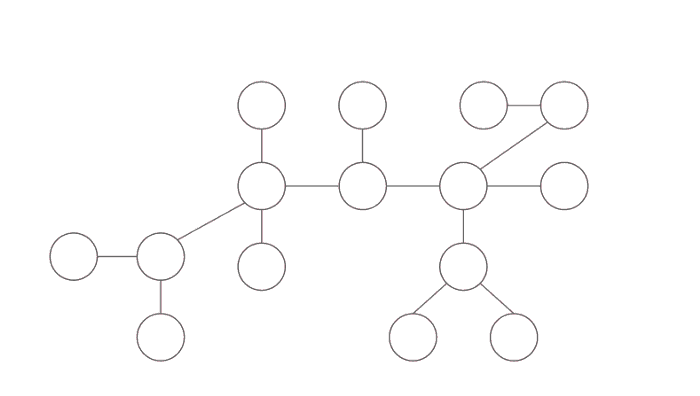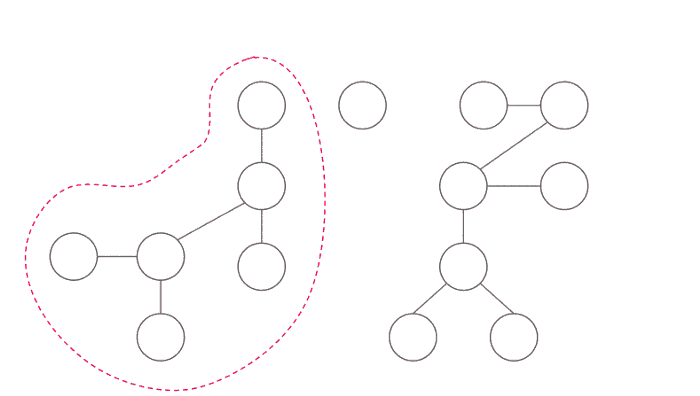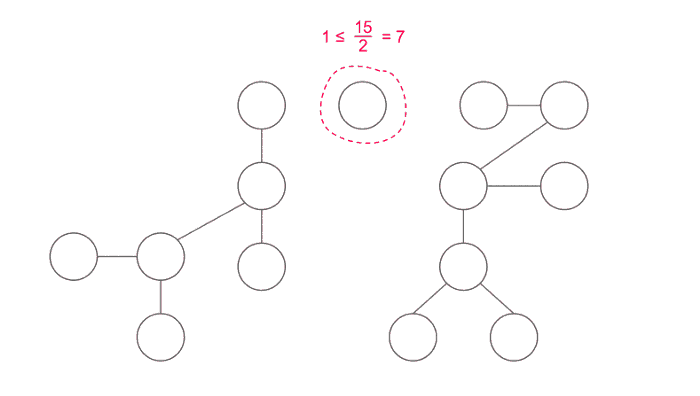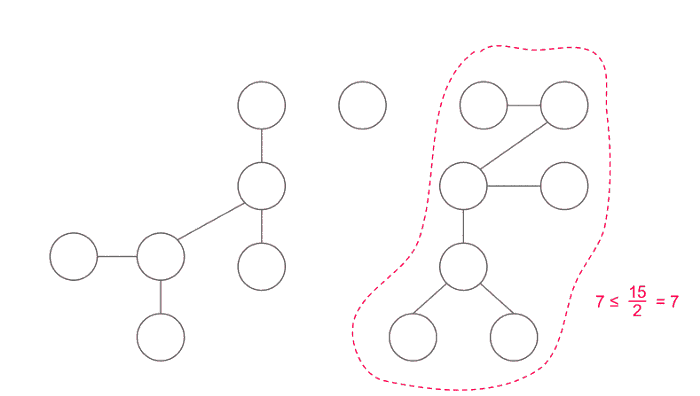
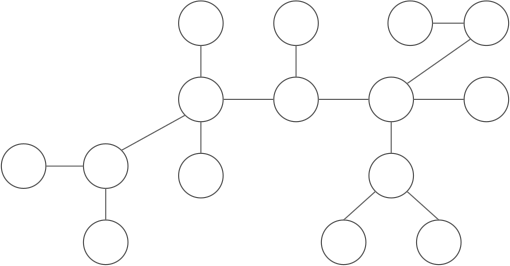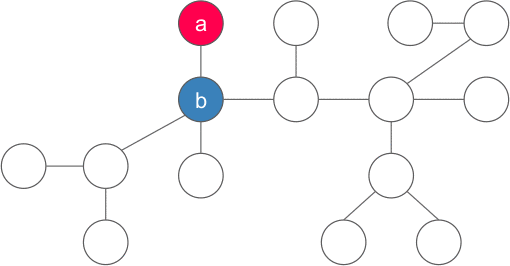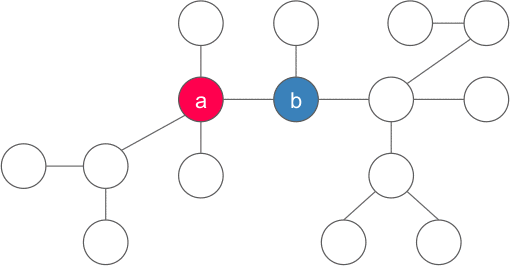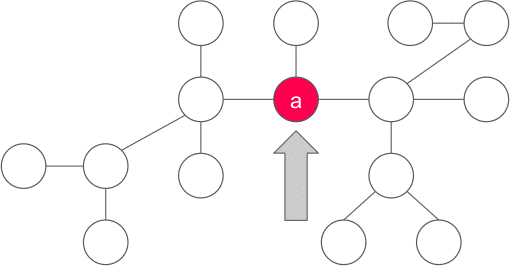
Centroid of the tree is different than centre of tree(centre of a tree is simply the middle vertex/vertices of the diameter of the tree). Centre of the tree is the node such that if rooted minimizes the height of the rooted tree. The centre of the tree in the middle of the largest path in the tree. In the following image blue node is the centre of the tree whereas the red node is the centroid of the tree.

Existence: Is there always a centroid? Yes. Every tree has at least one centroid.

Theorem (Jordan, 1869): Given a tree with N nodes, there exists a vertex whose removal partitions the tree into components, each with at most N/2 nodes. (i.e. For any given tree, the centroid always exists)

Proof: Let us chose any arbitrary vertex a in the tree, if a satisfies the property of the centroid, then we are done, else there exists one (and only one - if two such nodes exists then size of tree is > N) component with more than N/2 vertices. We now consider the vertex b adjacent to a in that component and apply the same argument for b . We continue the same procedure unless we find the required vertex. Also, we never go back to any old vertices because the component containing them must have less than N/2 vertices(because the subtree of b contains size > N/2). Since the no of vertices are finite, and we visit each vertex at most once, the procedure must end at the desired vertex and hence the centroid must exist.

Finding the centroid of a tree: One way to find the centroid is to pick an arbitrary root, then run a depth-first search computing the size of each subtree, and then move starting from root to the largest subtree until we reach a vertex where no subtree has size greater than N/2. This vertex would be the centroid of the tree.

Without storing size of subtrees, saving memory. source: Pavel marvin

# To calculate size of this component
def dfs_size(x, p):
    s = 1
    for y in Adj[x]:
        if y != p:
	    s += dfs_size(y, p)
    return s
    
def dfs_centroid(x, p):
    s = 1
    ok = True
    for y in Adj[x]:
    	if y != p:
	    sz_y = dfs_centroid(y, x)
	    if sz_y > n/2:
	        ok = False
	    s += sz_y
    if s < n/2: # checking for n - s ≤ n/2
        ok = False
    if ok:
        centroid = x # global variable
    return s
    
# To compute centroid
n = dfs_size(v, -1)
dfs_centroid(v, -1)

CPP: https://codeforces.com/contest/293/submission/27285541

The following stores subtree sizes and makes code simpler

vector<int> Adj[maxn];
int sub[maxn]; // subtree size

int dfs_sz(int u, int p) {
    for (int v : Adj[u])
        if (v != p) sub[u] += dfs_sz(v, u);
	
    return sub[u] + 1;
}

int centroid(int u, int p) {
    for (int v : Adj[u])
        if (v != p and sub[v] > n/2) return centroid(v, u);

    return u;
}

Um_nik's recursive implementation

const int N = 100100;
vector < int > g[N];
int sz[N];

void dfs(int v) {
    sz[v] = 1;
    for (int u: g[v]) {
        if (sz[u] != 0) continue;
        dfs(u);
        sz[v] += sz[u];
    }
}

int getCentroid(int v) // v - any vertex of tree
{
    dfs(v);
    while (true) {
        int w = -1;
        for (int u: g[v]) {
            if (sz[u] > sz[v]) continue;
            if (2 * sz[u] >= n) {
                w = u;
                break;
            }
        }
        if (w == -1) break;
        v = w;
    }
    return v;
}

Since we have found a centroid, there can atmost be one more centroid with subtree size exactly O(n/2) therefore we can find it as follows

vector<int> getCentroids(int v) // v - any vertex of tree
{
    v = getCentroid(v);
    vector < int > res;
    res.push_back(v);
    for (int u: g[v]) {
        if (2 * sz[u] == n)
            res.push_back(u);
    }
    return res;
}

source: https://um-nik.github.io/centroid

Centroid Decomposition

On removing the centroid, the given tree decomposes into a number of different trees, each having no of nodes < N/2 . We make this centroid the root of our centroid tree and then recursively decompose each of the new trees formed and attach their centroids as children to our root. Thus , a new centroid tree is formed from the original tree.

Centroid Decomposition works by repeated splitting the tree and each of the resulting subgraphs at the centroid, producing O(log N) layers of subgraphs. Since at each step, the new trees formed by removing the centroid have size at-most N/2, the maximum no of levels would be O(log N). Hence, the height of the centroid tree would be at most O(log N).

Decomposing the Original Tree to get Centroid Tree

def decompose(root, centroid_parent = -1):
    centroid = find_centroid(root)
    if centroid_parent != -1:
    	add_edge_in_centroid_tree(centroid_parent, centroid)
    for (adjacent_edge, adjacent_vertex) in G[centroid]:
    	delete_edge(adjacent_edge)
	decompose(adjacent_vertex, centroid)

source: Indian Programming Camp 2020, Thanuj Khattar

Let's mark the centroid with label 0, and remove it. After removing the centroid the tree separates into several parts of size at most N/2. Naturally, now we do the same recursively for each part, only marking the new centroids with label 1, then we get even more parts of size at most N/4, mark their centroids with label 2, and so on, until we reach parts of size 1. Since the size decreases at least twice with each step, the labels will be at most log(N).

Observation 1: Time Complexity of Centroid decomposition: O(NlogN)

Observation 2: A vertex belongs to the component(in the original tree) of all its ancestors in the centroid tree. For example: The node 14 belongs to the component of 14, 15, 11 and 3.

• It's simple if we think in terms of descendants instead of ancestors. The node a is a descendant of node b if a belong to the subtree resulting after removal of b. Note that the removal of b will only affect its own component/subtree, because we already disconnected b from its parent in the centroid decomposition. This means that all the descendants of b belong to its component.

Observation 3: Consider any two arbitrary vertices a and b and the path between them (in the original tree) can be broken down into path from a to lca(a,b) and the path from lca(a,b) to b, where lca(a,b) is the lowest common ancestor of a and b in the centroid tree. For example: The path from 9 to 10 in the original tree can be decomposed into the path from 9 to 3 and the path from 3 to 10.

• It is not hard to see that given any arbitray vertices a and b and their lca(a, b) in the centroid tree, both a and b lie inside the part which the vertex lca(a, b) was centroid of, and they were first separated into different parts when the vertex lca(a, b) was removed.
• Both a and b belong to the component(subtree) where the node lca(a,b) is the centroid. Suppose, by contradiction, that lca(a,b) doesn’t divide the path from a to b into two disjoint parts. It means that both a and b will be in the same component(subtree) after the removal of lca(a,b) in the original tree. Consequently, the centroid of that component would be a common ancestor of a and b lower than lca(a,b) which is contradiction.
• Another way to think about it is that, any path from a to b can be split into a to c and c to b, where c is some centroid. How to find this vertex c? Consider the centroid at level 0, if a and b are in the same component then go to that component, if not then this centroid divides path a and b into two parts.

Observation 4: We decompose the given tree into O(NlogN) different paths (from each centroid to all the vertices in the corresponding part) such that any path in the original tree is a concatenation of two different paths from this set. (This is the most important/new/extra part in this Data Structure(DS) that should be focused on).

• Using some DS, we maintain the required information (based on the problem) about these O(NlogN) different paths chosen such that any other path can be decomposed into 2 different paths from this set and these two paths can be found in O(logN) time, by finding the LCA in the centroid tree (since height of centroid tree is at most O(logN), we can find the LCA by just moving up from the deeper node).
• Each path from a to b in the original tree can be represented path from a -> lca(a, b) and lca(a, b) -> b. For each node we have O(logN) ancestors becuase the height of tree is O(logN). There are N nodes in total and hence number of paths in O(NlogN), that is there are only O(NlogN) paths from every node to its ancestors.

Pavel Marvin Implementation

# To calculate size of this component
def dfs_size(x, p):
    if deleted[x]:
    	return 0
    s = 1
    for y in Adj[x]:
        if y != p:
	    s += dfs_size(y, p)
    return s
    
def dfs_centroid(x, p):
    if deleted[x]:
    	return 0
    s = 1
    ok = True
    for y in Adj[x]:
    	if y != p:
	    sz_y = dfs_centroid(y, x)
	    if sz_y > n/2:
	        ok = False
	    s += sz_y
    if s < n/2: # checking for n - s ≤ n/2
        ok = False
    if ok:
        centroid = x # global variable
    return s
    
def solve(v):
    n = dfs_size(v, -1) # size of this subtree
    dfs_centroid(v, -1) # find centroid of this subtree
    c = centroid
    deleted[c] = True
    calculate(c) # depends on problem, what info to store
    for u in Adj[c]:
        if not deleted[u]:
	    solve(u) # recursively decompose

Carpanese implementation

Using vector<set> for Adjacency list, see Baba's implementation below for Distance in the Tree for better implementation.

struct CentroidDecomposition {
	vector<set<int>> tree; // it's not vector<vector<int>>!
	vector<int> dad; // parent in centroid tree
	vector<int> sub; // subtree size in original tree

	CentroidDecomposition(vector<set<int>> &tree) : tree(tree) {
		int n = tree.size();
		dad.resize(n);
		sub.resize(n);
		build(0, -1);
	}

	void build(int u, int p) {
		int n = dfs(u, p); // find the size of each subtree
		int centroid = dfs(u, p, n); // find the centroid
		if (p == -1) p = centroid; // dad of root is the root itself
		dad[centroid] = p;

		// for each tree resulting from the removal of the centroid
		for (auto v : tree[centroid])
			tree[centroid].erase(v), // remove the edge to disconnect
			tree[v].erase(centroid), // the component from the tree
			build(v, centroid);
	}

	int dfs(int u, int p) {
		sub[u] = 1;

		for (auto v : tree[u])
			if (v != p) sub[u] += dfs(v, u);

		return sub[u];
	}

	int dfs(int u, int p, int n) { // find centroid in the subtree of size n
		for (auto v : tree[u])
			if (v != p and sub[v] > n/2) return dfs(v, u, n);

		return u;
	}

	int operator[](int i) {
		return dad[i];
	}
};

Problems & Analysis

The problems that can be solved by Centroid decomposition can be categorised into

• Activating nodes(Xenia and Tree, QTREE5, YATP)
• Computing function for all paths(IOI 2011 Race, how many paths have xor k, Sum of all xor path in a tree)
• Computing function from all other subtrees and paths(PrimeDST, CF #107 Div1 E. Freezing with Style)
• Radius query around a vertex(Tree query)

CF 199 Div 2 E. Xenia and Tree

https://codeforces.com/contest/342/problem/E

Given a tree of n nodes indexed from 1 to n. The first node is initially painted red, and the other nodes are blue.

We should execute two types of queries:

• paint a specified blue node to red
• calculate which red node is the closest to the given one and print the shortest distance to the closest red node.

Using Centroid decomposition, O(lg²(n)) per query

• Let ans[a] be the distance to the closest rose node to a in the component where node a is centroid. Initially, ans[a] = ∞ because all nodes are blue (we’ll update the first node before reading the operations).
• For each update(a), we do ans[b] = min(ans[b], dist(a, b)) for every ancestor b of a in centroid tree, where dist(a,b) is the distance in the original tree.
• The time complexity of update is O(lg²(n)) because we are moving up on the tree of height lg(n) and for each step we evaluate dist(a,b) in O(lg(n)). We can do it in O(lg(n)), see Tanuj Baba's implementation.
• For each query(a), we take the minimum of dist(a,b) + ans[b] for every ancestor b of a, where dist(a,b) is the distance in the original tree.

The below solution is not efficient as it uses set for Adjacency list and map for distance. See Tanuj's implementation.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = (int)1e5 + 5;
const int inf = (int)1e9;

struct CentroidDecomposition {
  set<int> G[N];
  map<int, int> dis[N];
  int sz[N], pa[N], ans[N];

  void init(int n) {
    for(int i = 1 ; i <= n ; ++i) G[i].clear(), dis[i].clear(), ans[i] = inf;
  }
  void addEdge(int u, int v) {
    G[u].insert(v); G[v].insert(u);
  }
  int dfs(int u, int p) {
    sz[u] = 1;
    for(auto v : G[u]) if(v != p) {
      sz[u] += dfs(v, u);
    }
    return sz[u];
  }
  int centroid(int u, int p, int n) {
    for(auto v : G[u]) if(v != p) {
      if(sz[v] > n / 2) return centroid(v, u, n);
    }
    return u;
  }
  void dfs2(int u, int p, int c, int d) { // build distance 
    dis[c][u] = d;
    for(auto v : G[u]) if(v != p) {
      dfs2(v, u, c, d + 1);
    }
  }
  void build(int u, int p) {
    int n = dfs(u, p);
    int c = centroid(u, p, n);
    if(p == -1) p = c;
    pa[c] = p;
    dfs2(c, p, c, 0);

    vector<int> tmp(G[c].begin(), G[c].end());
    for(auto v : tmp) {
      G[c].erase(v); G[v].erase(c);
      build(v, c);
    }
  }
  void modify(int u) {
    for(int v = u ; v != 0 ; v = pa[v]) ans[v] = min(ans[v], dis[v][u]);
  }
  int query(int u) {
    int mn = inf;
    for(int v = u ; v != 0 ; v = pa[v]) mn = min(mn, ans[v] + dis[v][u]);
    return mn;
  }
} cd;

int n, q;

void init() {
  cin >> n >> q;
  cd.init(n);
  for(int i = 0 ; i < n - 1 ; ++i) {
    int a, b; cin >> a >> b; cd.addEdge(a, b);
  }
  cd.build(1, 0);
}
void solve() {
  cd.modify(1);
  int t, u;
  while(q--) {
    cin >> t >> u;
    if(t == 1) cd.modify(u);
    else cout << cd.query(u) << '\n';
  }
}

int main() {
  ios_base::sync_with_stdio(0), cin.tie(0);
  init();
  solve();
}

Using Centroid decomposition, O(lg(n)) per query

• Let ans[i] denote the min distance to a red node for the centroid "i" in it's corresponding part. Hence initially, let ans[i]=INF, for all i.
• For each update , to paint a node u red, we move up to all the ancestors x of u in the centroid tree and update their ans as, ans[x] = min(ans[x], dist(x,u)) because node u will be in the part of all the ancestors of u.
• For each query, to get the closest red node to node u, we again move up to all the ancestors of u in the centroid tree and take the minimum as: mn = min(mn, dist(x,u) + ans[x] );
• Why would this work ?? Let x be the closest red node to u in the graph. If x lies in the part of u, dist(u,u) + ans[u] would give the minimum distance and all it's ancestor's would give a distance greater than this , hence the minimum would not be affected. Same argument would work if x lies in any one of the ancestors of u. Also, x must lie in the part of any one ancestor because the root node of centroid tree represents the whole tree.
• An interesting observation/optimization to remove the extra additive O(logN) factor is that we only need distance between a node and all it's ancestors in the centroid tree. Also, if we root a tree at it's centroid, we can get distances from centroid to all other nodes in the tree. Hence, we maintain a "dist[LOGN][N]" array such that dist[i][j] is the distance of node j from the root in the i'th level of decomposition. Hence, now the distance of a node to it's ancestor can be found in O(1) using the above information but building this dist array also means an extra additive O(n) at each O(logN) levels of decomposition.

const int nax = 1e5 + 10;
const int LG = 20;

vector<int> Adj[nax];

int deleted[nax], sub[nax];
int par[nax], level[nax]; // centroid tree
int dist[LG][nax]; // dist[level][node], dist to i-th level centroid
int ans[nax]; // answer at this centroid

int dfs_sz(int u, int p){
    int sz = 1;
    for(int v:Adj[u])
        if(!deleted[v] && v!=p) sz += dfs_sz(v, u);
    return sub[u] = sz;
}

int find_centroid(int u, int p, int sz){
    for(int v:Adj[u]){
        if(deleted[v] || v==p) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u; // no subtree has size > sz/2
}

// calcuate distances from centroid in original tree
void calculate(int u, int p, int lvl){
    for(int v:Adj[u]){
        if(deleted[v] || v==p) continue;
        dist[lvl][v] = dist[lvl][u] + 1;
        calculate(v, u, lvl);
    }
}

// decompose the original tree
void decompose(int u, int p){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);
    par[centroid] = p; // for level 0 centroid, parent will be 0
    level[centroid] = level[p] + 1;

    calculate(centroid, p, level[centroid]);

    deleted[centroid] = true; // remove centroid
    for(int v:Adj[centroid])
        if(v != p && !deleted[v]) decompose(v, centroid);
}

///////// Queries //////////////

// Paint a specific node red
void paint(int u){
    int x = u;
    while(x != 0){
        ans[x] = min(ans[x], dist[level[x]][u]);
        x = par[x];
    }
}

// find nearest red node
int query(int u){
    int ret = INT_MAX;
    int x = u;
    while(x != 0){
        ret = min(ret, ans[x] + dist[level[x]][u]);
        x = par[x];
    }
    return ret;
}

int main() {
    int n, q;
    scanf("%d%d", &n, &q);
    for(int i=0;i<n-1;i++){
        int u, v; // 1-based indexing
        scanf("%d%d", &u, &v);
        Adj[u].push_back(v);
        Adj[v].push_back(u);
    }
    level[0] = -1;
    decompose(1, 0);

    for(int i=1;i<=n;i++) ans[i] = INF;
    paint(1);
    while(q--){
        int type, v;
        scanf("%d%d", &type, &v);
        if(type == 1){
            paint(v);
        }else{
            printf("%d\n", query(v));
        }
    }
	return 0;
}

source: Inspired from Baba's implementation https://codeforces.com/contest/342/submission/11945201 and https://pastebin.com/YPhMK9Dg (See Timus problem code below)

QTREE5 - SPOJ

You are given a tree (an acyclic undirected connected graph) with N nodes. The tree nodes are numbered from 1 to N. We define dist(a, b) as the number of edges on the path from node a to node b.

Each node has a color, white or black. All the nodes are black initially.

We will ask you to perfrom some instructions of the following form:

• 0 i : change the color of i-th node(from black to white, or from white to black).
• 1 v : ask for the minimum dist(u, v), node u must be white(u can be equal to v). Obviously, as long as node v is white, the result will always be 0.

Using centroid decomposition, O(lg²(n)) per query

• A very similar problem as above. The only difference is that now, we can even revert back to the original colour.
• Hence we might maintain a multiset for each node instead of just one minimum distance and process the queries in a very similar way as above.
• Time complexity ? O(log^2 N) (with an extra "additive" O(logN) factor per query/update because of the multiset)

const int nax = 1e5 + 10;
const int LG = 20;

vector<int> Adj[nax];

int deleted[nax], sub[nax];
int par[nax], level[nax]; // centroid tree
int dist[LG][nax]; // dist[level][node], dist to i-th level centroid
multiset<int> ans[nax]; // answer at this centroid
int col[nax];

int dfs_sz(int u, int p){
    int sz = 1;
    for(int v:Adj[u])
        if(!deleted[v] && v!=p) sz += dfs_sz(v, u);
    return sub[u] = sz;
}

int find_centroid(int u, int p, int sz){
    for(int v:Adj[u]){
        if(deleted[v] || v==p) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u; // no subtree has size > sz/2
}

// calcuate distances from centroid in original tree
void calculate(int u, int p, int lvl){
    for(int v:Adj[u]){
        if(deleted[v] || v==p) continue;
        dist[lvl][v] = dist[lvl][u] + 1;
        calculate(v, u, lvl);
    }
}

// decompose the original tree
void decompose(int u, int p){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);
    par[centroid] = p; // for level 0 centroid, parent will be 0
    level[centroid] = level[p] + 1;

    calculate(centroid, p, level[centroid]);

    deleted[centroid] = true; // remove centroid
    for(int v:Adj[centroid])
        if(v != p && !deleted[v]) decompose(v, centroid);
}

///////// Queries //////////////

// Paint a specific node
void paint(int u){
    if(col[u] == 1){ // white
        int x = u;
        while(x != 0){
            ans[x].erase(ans[x].lower_bound(dist[level[x]][u]));
            x = par[x];
        }
    }else{
        int x = u;
        while(x != 0){
            ans[x].insert(dist[level[x]][u]);
            x = par[x];
        }
    }
    col[u] = 1 - col[u];
}

// find nearest red node
int query(int u){
    int ret = INF;
    int x = u;
    while(x != 0){
        if(SZ(ans[x]) > 0) ret = min(ret, *ans[x].begin() + dist[level[x]][u]);
        x = par[x];
    }
    if(ret == INF) return -1;
    return ret;
}

int main() {
    int n, q;
    scanf("%d", &n);
    for(int i=0;i<n-1;i++){
        int u, v; // 1-based indexing
        scanf("%d%d", &u, &v);
        Adj[u].push_back(v);
        Adj[v].push_back(u);
    }
    level[0] = -1;
    decompose(1, 0);

    scanf("%d", &q);
    while(q--){
        int type, v;
        scanf("%d%d", &type, &v);
        if(type == 0){
            paint(v);
        }else{
            printf("%d\n", query(v));
        }
    }
	return 0;
}

Distance in the Tree - Timus

A weighted tree is given. You must find the distance between two given nodes.

Input

The first line contains the number of nodes of the tree n (1 ≤ n ≤ 50000). The nodes are numbered from 0 to n – 1. Each of the next n – 1 lines contains three integers u, v, w, which correspond to an edge with weight w (0 ≤ w ≤ 1000) connecting nodes u and v. The next line contains the number of queries m (1 ≤ m ≤ 75000). In each of the next m lines there are two integers.

Using centroid decomposition

Given a tree with N nodes and Q queries of the form u v - Return the sum of elements on the path from u to v.

Instead of using set<int> Adj and deleting the actual edges, if we use deleted[v] marker then it is easy to delete. Also note instead of using map<int,int> for dist function, we can use dist[lvl][maxn] and store distance to of it's ancestor and get rid of one log factor.

// Accepted code for https://acm.timus.ru/problem.aspx?space=1&num=1471
#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

const int N = 1e5 + 10;
const int LOGN = 20;
// Original Tree
vector<int> g[N];
int sub[N], nn, U[N], V[N], W[N], deleted[N];
// Centroid Tree
int par[N], level[N], dist[LOGN][N];
// dist[LOGN][N] : dist[lvl][x] :  Distance between C and x in the original tree, when node C becomes a centroid at level "lvl". 
// G[u] --> [v1, v2, v3] ... Not doing this.
// G[u] --> [e1, e1, e3 ..] 
int adj(int x, int e) { return U[e] ^ V[e] ^ x; } // find the other end of this edge
void dfs1(int u, int p) { // to calculate size of subtrees
  sub[u] = 1;
  nn++; // global variable
  for (auto e : g[u]) {
    int w = adj(u, e);
    if (w != p && !deleted[e]) dfs1(w, u), sub[u] += sub[w];
  }
}
int find_centroid(int u, int p) {
  for (auto e : g[u]) {
    if (deleted[e]) continue;
    int w = adj(u, e);
    if (w != p && sub[w] > nn / 2) return find_centroid(w, u);
  }
  return u; // if not subtree has size > nn/2, then u is the centroid
}
void add_edge_centroid_tree(int parent, int child) {
  // this func depends on the information to store in the question
  par[child] = parent;
  level[child] = level[parent] + 1; // level in centroid tree
}
void dfs2(int u, int p, int lvl) {
  for (auto e : g[u]) {
    int w = adj(u, e);
    if (w == p || deleted[e]) continue;
    dist[lvl][w] = dist[lvl][u] + W[e]; // key to make implementation efficient
    dfs2(w, u, lvl);
  }
}

// unordered_map<int, int> dist[N]; -- inefficient.
// all the nn nodes which lie in the component of "centroid"
// dist[centroid][x] = <value>
// int dist[LOGN][N]; (centroid,x) --> one to one mapping --> (level[centroid], x);
void decompose(int root, int p = -1) {
  nn = 0; // size of subtree of which this decompose is being called
  // Compute subtree sizes and no. of nodes (nn) in this tree.
  dfs1(root, root);
  // Find the centroid of the tree and make it the new root.
  int centroid = find_centroid(root, root);
  // Construct the Centroid Tree
  if (p == -1) p = root; // p = centroid, parent of centroid is centroid
  add_edge_centroid_tree(p, centroid);
  // Process the O(N) paths from centroid to all leaves in this component.
  dfs2(centroid, centroid, level[centroid]);
  // Delete the adjacent edges and recursively decompose the adjacent subtrees.
  for (auto e : g[centroid]) {
    if (deleted[e]) continue;
    deleted[e] = 1;
    int w = adj(centroid, e);
    decompose(w, centroid);
  }
}

int compute_distance(int x, int y) {
  // We need to compute the LCA(x, y) in the centroid tree. 
  // Height of centroid tree is O(logN), so can compute in brute force way.
  int lca_level = 0;
  for (int i = x, j = y; (lca_level = level[i]) && i != j;
       level[i] < level[j] ? (j = par[j]) : (i = par[i]))
    ;
  return dist[lca_level][x] + dist[lca_level][y];
}

int main() {
  int n;
  scanf("%d", &n);
  for (int i = 1; i < n; i++) {
    // Adj List & Edge list representation
    // i-th edges goes from U[i] to V[i] and has weight W[i]
    scanf("%d %d %d", U + i, V + i, W + i);
    U[i]++; V[i]++; // one based indexing
    g[U[i]].push_back(i); // pushing edge number instead of vertex
    g[V[i]].push_back(i);
  }
  decompose(1); // calling centroid decomposition on arbitrary vertex
  int m;
  scanf("%d", &m);
  while (m--) {
    int x, y;
    scanf("%d %d", &x, &y);
    printf("%d\n", compute_distance(x + 1, y + 1));
  }
}

Radius Query Problem - Codeforces Hunger games Tree Query

You are give a weighted tree with vertices 1 to n. You have to answer q queries of the form query(v, l) and you should tell him the number of vertexes like u such that d(v, u) ≤ l (including v itself).

source: https://codeforces.com/group/qcIqFPYhVr/contest/203881/problem/X

Using centroid decomposition

• Decompose the tree and for every centroid, maintain the number of nodes at distance d for every d(e.g: sorted array subtree in the code)
  • i.e Support queries of the form "How many nodes nodes x are there s.t dist(x, c) ≤ d" for a given centroid.
• Also maintain the "contribution" of a centroid to the subtree array of it's parent centroid in the centroid tree. This is used to avoid double counting of the nodes which are in the same subtree as x. See postprocess phase in the solution.
  • i.e Support queries of the form "How many nodes x are there s.t dist(x, par[c]) ≤ d and x lies in the subtree of c"
• To answer a query for the node x, start with x in the centroid tree and go up to all it's ancestors, adding the number of nodes at distance d - dist[anc][x] in the section of centroid p wihout overcounting the nodes already considered in the child. In the code this is ans += within_dist(par[x], t) - sub_within_dist(x, t); or POSU(subtree[par[c]], td) - POSU(cbn[c], td);

The key idea is in the postprocess phase of this solution.

const int nax = 1e5 + 10;
const int LG = 20;

vector<pair<int,int>> Adj[nax];

bool deleted[nax];
int sub[nax], level[nax], par[nax];
long long dist[LG][nax];
vector<long long> subtree[nax]; // distances of nodes in subtree
vector<long long> cnbtn[nax]; // contribution of this subtree to its parent

int dfs_sz(int u, int p = 0){
    int sz = 1;
    for(auto [v, w] : Adj[u]){
        if(deleted[v] || v == p) continue;
        sz += dfs_sz(v, u);
    }
    return sub[u] = sz;
}

int find_centroid(int u, int p, int sz){
    for(auto [v, w]: Adj[u]){
        if(v == p || deleted[v]) continue;
        if(sub[v] > sz/2)
            return find_centroid(v, u, sz);
    }
    return u;
}

void calculate(int u, int p, int lvl){
    for(auto [v, w]: Adj[u]){
        if(deleted[v] || v == p) continue;
        dist[lvl][v] = dist[lvl][u] + w;
        calculate(v, u, lvl);
    }
}

void decompose(int u, int p = 0){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);

    level[centroid] = level[p] + 1;
    par[centroid] = p; // parent in centroid tree
    deleted[centroid] = 1;

    calculate(centroid, p, level[centroid]);

    for(auto [v, w]: Adj[centroid]){
        if(v == p || deleted[v]) continue;
        decompose(v, centroid);
    }
}

void postprocess(int n){
    for(int x = 1; x <= n; x++){
        for(int y = x; y; y = par[y]){
            // add node in subtree of level[y] centroid
            subtree[y].push_back(dist[level[y]][x]);
            // contribution of subtree of centroid y towards it's parent
            if(par[y]) cnbtn[y].push_back(dist[level[par[y]]][x]);
        }
    }

    for(int x = 1; x <= n; x++){
        sort(subtree[x].begin(), subtree[x].end());
        sort(cnbtn[x].begin(), cnbtn[x].end());
    }
}

#define POSU(x,v) (upper_bound(x.begin(),x.end(),v)-x.begin())

// nodes within distance d in subtree of x in centroid tree
int within_dist(int u, long long d){
    return POSU(subtree[u], d);
}

// nodes from this subtree contributing to it's parent in centroid tree
int sub_within_dist(int u, long long d){
    return POSU(cnbtn[u], d);
}

int radius_query(int u, long long d){
    int ans = POSU(subtree[u], d);

    for(int x = u; par[x] > 0; x = par[x]){
        long long t = d - dist[level[par[x]]][u];
        ans += within_dist(par[x], t) - sub_within_dist(x, t);
    }
    return ans;
}

int main() {
    int n, q;
    scanf("%d %d", &n, &q);
    for(int i=0; i<n-1; i++){
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);
        Adj[a].push_back({b, w});
        Adj[b].push_back({a, w});
    }
    decompose(1);
    postprocess(n);
    while(q--){
        long long x, d;
        scanf("%lld %lld", &x, &d);
        printf("%d\n", radius_query(x, d));
    }
    return 0;
}

PRIMEDST - Codechef

You are given a tree. If we select 2 distinct nodes uniformly at random, what's the probability that the distance between these 2 nodes is a prime number?

source: https://discuss.codechef.com/t/primedst-editorial/2905

Using Centroid decomposition and FFT

We'll find number of pairs (u, v) such that dist(u, v) = i for all i = 1,2,..., N -1. Then only add prime distances to our answer.

similar problem: https://judge.yosupo.jp/problem/frequency_table_of_tree_distance, https://judge.yosupo.jp/submission/28296

Divide & Conquery approach: We can do centroid decomposition and solve recursively. For each child v of a centroid, we can find how many decendents are at each distance. This takes care of all the paths that start at a centroid and always move downwards, towards the decendents.

For all the other paths, we can do a convolution of the arrays of values stored at each child of centroid. Of course, the fastest way to convolve is using Fast Fourier Transforms for polynomial multiplication. When doing convolution we need to be careful to make sure that we don't double count or convolute children of same subtree.

Divide phase: Centroid decomposition, Conquer phase: FFT convolution

How to compute FFT?

Let A[i] be number of nodes have a distance i from centroid in subtree A, we can define B and C similarly. Then in polynomial form

The the number of paths of length i which pass through centroid can be computed as

Polynomial 1 is for counting the number of paths starting or ending in centroid. We need to remove A^2 because paths connecting nodes in A doesn't pass through the centroid. This way each path from (u, v) is counted twice, once by u and once by v.

Another way to compute these paths would be calculating one subtree after another, for example when we calculate the paths from subtree C, we will convolute polynomial C with nodes in A and B, this contribution would be (1 + A + B)C. 1 counts the paths starting at centroid and ending in C, A for couting paths starting at A and ending in C, similarly for B.

We can check that both the ways lead to same solution except that in first case each path is counted twice.

(1 + A + B + C)^2 - A^2 - B^2 - C^2 =  (A^2 + B^2 + C^2 + 1 + 2AB + 2BC + 2AC + 2A + 2B + 2C) - A^2 - B^2 - C^2 
                                    = 1 + 2AB + 2BC + 2AC + 2A + 2B + 2C
				    = 1 + 2(AB + BC + AC + A + B + C)
				    = 1 + 2( A + (1+A)B + (1+A+B)C )

// Convolution by FFT (Fast Fourier Transform)
// Algorithm based on <http://kirika-comp.hatenablog.com/entry/2018/03/12/210446>
// Verified: ATC001C (168 ms) <https://atcoder.jp/contests/atc001/submissions/9243440>
using cmplx = complex<double>;
void fft(int N, vector<cmplx> &a, double dir)
{
    int i = 0;
    for (int j = 1; j < N - 1; j++) {
        for (int k = N >> 1; k > (i ^= k); k >>= 1);
        if (j < i) swap(a[i], a[j]);
    }

    vector<cmplx> zeta_pow(N);
    for (int i = 0; i < N; i++) {
        double theta = M_PI / N * i * dir;
        zeta_pow[i] = {cos(theta), sin(theta)}; // cosθ + isinθ
    }

    for (int m = 1; m < N; m *= 2) {
        for (int y = 0; y < m; y++) {
            cmplx fac = zeta_pow[N / m * y];
            for (int x = 0; x < N; x += 2 * m) {
                int u = x + y;
                int v = x + y + m;
                cmplx s = a[u] + fac * a[v];
                cmplx t = a[u] - fac * a[v];
                a[u] = s;
                a[v] = t;
            }
        }
    }
}
template<typename T>
vector<cmplx> conv_cmplx(const vector<T> &a, const vector<T> &b)
{
    int N = 1;
    while (N < (int)a.size() + (int)b.size()) N *= 2;
    vector<cmplx> a_(N), b_(N);
    for (int i = 0; i < (int)a.size(); i++) a_[i] = a[i];
    for (int i = 0; i < (int)b.size(); i++) b_[i] = b[i];
    fft(N, a_, 1);
    fft(N, b_, 1);
    for (int i = 0; i < N; i++) a_[i] *= b_[i];
    fft(N, a_, -1);
    for (int i = 0; i < N; i++) a_[i] /= N;
    return a_;
}
// retval[i] = \sum_j a[j]b[i - j]
// Requirement: length * max(a) * max(b) < 10^15
template<typename T>
vector<long long int> fftconv(const vector<T> &a, const vector<T> &b)
{
    vector<cmplx> ans = conv_cmplx(a, b);
    vector<long long int> ret(ans.size());
    for (int i = 0; i < (int)ans.size(); i++) ret[i] = floor(ans[i].real() + 0.5);
    ret.resize(a.size() + b.size() - 1);
    return ret;
}

const int nax = 5e4+10;
const int LG = 20;

vector<int> Adj[nax];

int deleted[nax], sub[nax];

long long paths[nax]; // paths[i] = number of paths with distance i
vector<long long> cnt;

int dfs_sz(int u, int p){
    int sz = 1;
    for(int v:Adj[u])
        if(!deleted[v] && v!=p) sz += dfs_sz(v, u);
    return sub[u] = sz;
}

int find_centroid(int u, int p, int sz){
    for(int v:Adj[u]){
        if(deleted[v] || v==p) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u; // no subtree has size > sz/2
}

// calcuate distances from centroid in original tree
void calculate(int u, int p, int d){
    while(cnt.size() <= d) cnt.push_back(0);
    cnt[d]++; // there exists one more path of length d from centroid
    for(int v:Adj[u])
        if(v != p && !deleted[v]) calculate(v, u, d+1);
}

// decompose the original tree
void decompose(int u, int p){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);

    // paths[i] = number of paths starting at this centroid and having len i
    vector<long long> c_paths = {1};

    for(int v:Adj[centroid]){
        if(v==p || deleted[v]) continue;

        cnt.clear();
        calculate(v, centroid, 1);

        if(c_paths.size() < cnt.size()) c_paths.resize(cnt.size());
        for(int i=0;i<cnt.size();i++) c_paths[i] += cnt[i];
        
        if(cnt.size() == 0) continue;
        vector<long long> cnt2 = fftconv(cnt, cnt);
        for(int i=0;i<cnt2.size();i++)
            paths[i] -= cnt2[i];
    }

    vector<long long> c_paths2 = fftconv(c_paths, c_paths);
    for(int i=0;i<c_paths2.size();i++)
        paths[i] += c_paths2[i];

    deleted[centroid] = true; // remove centroid
    for(int v:Adj[centroid])
        if(v != p && !deleted[v]) decompose(v, centroid);
}


int main() {
    int n;
    scanf("%d", &n);
    for(int i=0;i<n-1;i++){
        int u, v; // 1-based indexing
        scanf("%d%d", &u, &v);
        Adj[u].push_back(v);
        Adj[v].push_back(u);
    }
    decompose(1, 0);

    vector<bool> prime(n, true);
    prime[0] = prime[1] = false;
    for(int i=2;i<n;i++)
        if(prime[i])
            for(int j=2*i;j<n;j+=i) prime[j] = false;

    long long total = 1ll*n*(n-1)/2;
    long double valid = 0;
    for(int i=0;i<n;i++)
        if(prime[i])
            valid += paths[i]/2; // (u, v) and (v, u) are same

    printf("%0.8Lf\n", valid/total);
}

Another way of computing the same is to convolute values of previous subtrees.

void decompose(int u, int p){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);
    
    // prev_paths[i] = centroid to v of lent i till current subtree
    vector<long long> prev_paths = {1};

    for(int v:Adj[centroid]){
        if(v==p || deleted[v]) continue;

        cnt.clear();
        calculate(v, centroid, 1);

        if(cnt.size() == 0) continue;
        vector<long long> temp = fftconv(prev_paths, cnt);
        for(int i=0;i<temp.size();i++)
            paths[i] += temp[i];
        
        if(cnt.size() > prev_paths.size()) prev_paths.resize(cnt.size());
        for(int i=0;i<cnt.size();i++) prev_paths[i] += cnt[i];
    }

    deleted[centroid] = true; // remove centroid
    for(int v:Adj[centroid])
        if(v != p && !deleted[v]) decompose(v, centroid);
}

// inside main
    valid += paths[i]; // (u, v) is counted only once

Binarizing the given tree before decomposition

The given tree is not necessarily a binary tree. If we try to find a split of nodes in such a tree, we may end up with a split that selects only O(N / D) vertices in one set; here D is the largest degree of any node(see the below example, centroid has a subtree of size N/2 - 1 and sqrt(N) subtrees of size sqrt(N/2)). This would mean that our divide and conquer may perform too many FFTs in the worst case. This is highly undesirable.

For example: In the above subtree, the degree of the centroid is sqrt(N) + 1, hence we will need to do perform FFT sqrt(N) + 1 times and each FFT can take upto O(NlogN) time, because there is a subtree of size N/2 - 1 = O(N). Hence the time complexity might become O(N sqrt(N) log(N)).

To overcome this issue, we convert the given tree T into an equivalent binary tree T' by adding extra dummy nodes such that degree of each node in the transformed tree T' is  ≤ 3, and the number of dummy nodes added is bounded by O(N).

Hence we perform centroid decomposition of this transformed tree T'. The centroid tree formed would have the following properties.

• The height of the centroid tree is O(logN)
• Each node in the centroid tree has ≤ 3 children

We can convert the given tree into binary tree as follows:

If a node has more than 2 chilren

• Give the node a new right child
• Connect the node to its right child with a 0 cost edge
• Move all but 1 child to the children of the new right child
• The remaining child will be the left child of the node

In the final tree, the meaning of distance will be replaced by the sum of the costs of edges, instead of the number of edges.

Now, we can always find a split that selects at least O(N/3) nodes in one set.

For inter subtree path, list up all the distances to the original nodes in each subtree. Find the solution using FFT.

TODO: http://p.ip.fi/EgoG and http://p.ip.fi/n8N-

Small to Large Merging

Problem: You are given a rooted tree consisting of n nodes. The nodes are numbered 1,2,…,n, and node 1 is the root. Each node has a color.

Your task is to determine for each node the number of distinct colors in the subtree of the node.

For each node, let's store a set containing only that node, and we want to merge the sets in the nodes subtree together such that each node has a set consisting of all colors in the nodes subtree. Doing this allows us to solve a variety of problems, such as query the number of distinct colors in each subtree.

How to merge two vectors/sets efficiently?

Naive solution

Suppose that we want merge two sets a and b of sizes n and m, respectively. One possiblility is the following:

for (int x: b) a.insert(x);

which runs in O(m log(m+n)) time, yielding a runtime of O(N²log N) in the worst case. If we instead maintain a and b as sorted vectors, we can merge them in O(n+m) time, but O(N²) is also too slow.

Better solution

With just one additional line of code, we can significantly speed this up.

if (a.size() < b.size()) swap(a,b);
for (int x: b) a.insert(x);

Note that swap exchanges two sets in O(1) time. Thus, merging a smaller set of size m into the larger one of size n takes O(m log n) time.

Claim: The solution runs in O(N log²N) time.

Proof: When merging two sets, you move from the smaller set to the larger set. If the size of the smaller set is X, then the size of the resulting set is at least 2X. Thus, an element that has been moved Y times will be in a set of size at least 2^Y, and since the maximum size of a set is N (the root), each element will be moved at most O(log N) times.

Full Code

#include <bits/stdc++.h>

using namespace std;

const int MX = 200005;

vector < int > adj[MX];
set < int > col[MX];
long long ans[MX];
void dfs(int v, int p) {
    for (int e: adj[v]) {
        if (e != p) {
            dfs(e, v);
            if (col[v].size() < col[e].size()) {
                swap(col[v], col[e]);
            }
            for (int a: col[e]) {
                col[v].insert(a);
            }
            col[e].clear();
        }
    }
    ans[v] = col[v].size();
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        col[i].insert(x);
    }
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--;
        v--;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs(0, -1);
    for (int i = 0; i < n; i++) {
        cout << ans[i] << " ";
    }
}

source: https://usaco.guide/plat/merging?lang=cpp, https://codeforces.com/blog/entry/63353?#comment-472816

You don't need to do any decomposition. Root the tree arbitrarily, and for each vertex u let Su be the multiset of lengths of paths starting in the subtree of u and ending in u. To compute it, initially Su = {0} (the empty path), and then for each child v of u we take l in Sv and add l + 1 to Su. If you merge small sets into larger sets this will run in O(n log²n) time (and O(nlogn) if you can resolve the + 1 by maintaining some additive constant for each Su).

Then, to count the number of paths, notice that each path has some highest vertex it passes through, so in u we can compute all paths whose highest vertex is u. When we take a value l in Sv we would like to find all paths coming from earlier subtrees of u that add up to a path of length at least k. But this is just a range query (count all values in the multiset Su that are at least k - (l + 1)). Note: do all range queries for Sv before merging it into Su. So our set should support order statistics queries. You can use a treap or the GNU order statistics tree for this.

Actually you can do it in O(n): you don't need sets, you can just return a vector (have depth 0 in the last element, so you can increase depth by pushing an element to the back). When we merge a smaller set to a larger set, the size of the larger set doesn't increase. Thus, every vertex contributes to only one merge. We can maintain prefix sums on counts at depths while merging.

The above solution works for a fixed k in O(n) time.

Accepted code for Fixed-Length Paths I https://cses.fi/problemset/result/2376131/ - Given a tree of n nodes, your task is to count the number of distinct paths that consist of exactly k edges.

const int nax = 2e5 + 10;

vector<int> Adj[nax];

int k;
long long ans = 0;

vector<int> dfs(int u, int p){
    vector<int> V;
    for(int v:Adj[u]){
        if(v == p) continue;
        vector<int> X = dfs(v, u);

        // Small to Large Merging
        if(V.size() < X.size()) swap(V, X);

        // number of paths of length >= k passing through u
        for(int i=0; i<X.size(); i++){
            // number of nodes at depth d = cnt
            int cnt = X[i]; if(i) cnt -= X[i-1];
            int d = X.size() - i;
            // search for nodes with depth atleast k - d
            if(d >= k) ans += 1ll*cnt * V.back();
            else {
                if(k - d > V.size()) break;
                ans += 1ll*cnt * V[V.size() - (k - d)];
            }
        }

        // Merge X with V
        for(int i=0; i<X.size(); i++){
            int depth = X.size() - i;
            int cnt = X[i];
            V[V.size() - depth] += cnt;
        }
    }

    // number of paths starting from u
    if(V.size() >= k)
        ans += V[V.size() - k];

    if(V.empty()) V.push_back(1);
    else V.push_back(V.back()+1);

    // V = Prefix_sum(number of vertices at depth in reversed order)
    return V;
}

// number of paths of length = k
long long query(int q){
    ans = 0; k = q;
    dfs(1, -1);
    long long t = ans; // number of paths of length >= q
    ans = 0; k = q + 1;
    dfs(1, -1); // number of path of length >= q+1
    return t - ans;
}

int main() {
    int n, q;
    scanf("%d%d", &n, &q);
    for(int i=0; i<n-1; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        Adj[a].push_back(b);
        Adj[b].push_back(a);
    }

    printf("%lld\n", query(q));

    return 0;
}

If the k is small, we can also use dynamic programming. source: https://codeforces.com/contest/161/problem/D

Let us hang the tree making it rooted. For every vertex v of the tree, let us calculate values d[v][lev] (0 ≤ lev ≤ k) — the number of vertices in the subtree, having distance lev to them. Note, that d[v][0] = 0.

Then we calculate the answer. It equals the sum for every vertex v of two values:

• The number of ways of length k, starting in the subtree of v and finishing in v. Obviously, it equals d[v][k].

• The number of ways of length k, starting in the subtree of v and finishing in the subtree of v. This equals the sum for every son u of v the value:
  

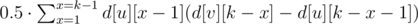
• Accumulate the sum for all vertices and get the solution in O(n·k).

CF #107 Div1 E. Freezing with Style

https://codeforces.com/contest/150/problem/E

The Nvodsk road system can be represented as n junctions connected with n - 1 bidirectional roads so that there is a path between any two junctions. The organizers of some event want to choose a place to accommodate the participants (junction v), and the place to set up the contests (junction u). Besides, at the one hand, they want the participants to walk about the city and see the neighbourhood (that's why the distance between v and u should be no less than l). On the other hand, they don't want the participants to freeze (so the distance between v and u should be no more than r). Besides, for every street we know its beauty — some integer from 0 to 10⁹. Your task is to choose the path that fits in the length limits and has the largest average beauty. We shall define the average beauty as a median of sequence of the beauties of all roads along the path.

Binary Search + Centroid Decomposition + Segment Tree

• If there exists a path with the median  ≥ k, for some k, then there exists a path with the median  ≥ q, for each q ≤ k. That means we can use binary search to calculate the answer. So now the task is: is there any path with the median greater or equal to Mid ?
• We will calc the edge as  + 1 if it's weight  ≥ Mid, or as  - 1 in other case. Now we only need to check if there exists a path with legal length and the sum greater than or equal to zero.
• Let's denote some node V as a root. All paths can be divided into two types: that contains v, and that do not. Now we are to process all first-type paths and run the algorithm on all subtrees. That is so-called divide-and-conquer strategy - Centroid Decomposition
• For each node we shall calculate it's deepnees(depth), cost of the path(dist) to the root. Now, for each node we want to know if there exists a node u in any other subtree such that the (cost[u] + cost[v] ≥ 0) and they are between [L, R] distance apart. We will need to find maximum of the function cost[u] with the deep values between max(0, L - deep[v]) and (R - deep[v]) inclusive. To achieve O(N * log(N)) you need only to use segment tree.

#include <bits/stdc++.h>
using namespace std;
 
const int nax = 1e5 + 10;
 
// Recursive segment tree
pair<int, int> rmq[nax * 2];
 
int rsz;
 
void build(int h) {
	++h;
	rsz = h;
	for (int i = 0; i < rsz - 1 + rsz; ++i)
		rmq[i] = make_pair(-nax * 100, -1);
}
 
pair<int, int> get(int l, int r) {
	l += rsz - 1;
	r += rsz - 1;
	pair<int, int> ans = make_pair(-nax * 100, -1);
	while (r > l) {
		if (l & 1) l = l >> 1;
		else ans = max(ans, rmq[l]), l = l >> 1;
		if (r & 1) r = r >> 1;
		else ans = max(ans, rmq[r - 1]), r = (r - 1) >> 1;
	}
	return ans;
}
 
void upd(int x, int c, int v) {
	x += rsz - 1;
	for (; x >= 0 && rmq[x].first < c; x = (x - 1) >> 1)
		rmq[x] = make_pair(c, v);
}
 
// Iterative version
pair<int, int> st[4*nax]; // max segment tree
 
pair<int, int> combine(pair<int, int> a, pair<int, int> b){
    return max(a, b);
}
 
// initialize segement tree with minimum
void build(int v, int l, int r){
    build(r+1);
    /* if(l == r){ */
    /*     st[v] = {-nax, l}; */
    /*     return; */
    /* } */
    /* int mid = (l+r)/2; */
    /* build(v*2, l, mid); */
    /* build(v*2+1, mid+1, r); */
    /* st[v] = combine(st[v*2], st[v*2+1]); */
}
 
// update pos with val
void update(int v, int l, int r, int pos, int val, int idx){
    upd(pos, val, idx);
    /* if(l==r){ */
    /*     st[v] = combine(st[v], {val, idx}); */
    /*     return; */
    /* } */
    /* int mid = (l+r)/2; */
    /* if(pos <= mid) update(v*2, l, mid, pos, val, idx); */
    /* else update(v*2+1, mid+1, r, pos, val, idx); */
    /* st[v] = combine(st[v*2], st[v*2+1]); */
}
 
// get max value in [L, R]
pair<int,int> get(int v, int l, int r, int L, int R){
    return get(L, R+1);
    /* if(L > R) return {-nax, L}; */
    /* if(l==L && r==R) return st[v]; */
    /* int mid = (l+r)/2; */
    /* return combine(get(v*2, l, mid, L, min(mid, R)), */
    /*             get(v*2+1, mid+1, r, max(L, mid+1), R)); */
}
 
/////// End of segment tree //////////
 
int U[nax], V[nax], W[nax];
int sub[nax];
int dist[nax], depth[nax];
bool deleted[nax];
vector<int> Adj[nax];
int weight;
 
int distl, distr;
bool ans;
pair<int, int> node_ans;
 
inline int adj(int u, int e){
    return U[e] ^ V[e] ^ u;
}
 
void preprocess(){
    ans = false;
    memset(deleted, 0, sizeof(deleted));
    memset(depth, 0, sizeof(depth));
}
 
int dfs_sz(int u, int p){
    sub[u] = 1;
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        sub[u] += dfs_sz(v, u);
    }
    return sub[u];
}
 
int find_centroid(int u, int p, int sz){
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u;
}
 
struct Node {
    int depth, cost, idx;
    Node(int x, int y, int z): depth(x), cost(y), idx(z) {}
};
 
ostream& operator<<(ostream& os, const Node n) { // useful for printing while debugging
    os << "{depth: " << n.depth << " cost: " << n.cost << " idx: " << n.idx << "}";
    return os;
}
 
vector<Node> children;
 
void calculate(int u, int p, int wedge){
    dist[u] = dist[p] + (wedge >= weight ? 1 : -1);
    depth[u] = depth[p] + 1;
    if(depth[u] > distr) return; // ignore nodes which are too deep
    // store only one Node for each depth
    if((int)children.size() < depth[u]){ // i-th node => (i+1) depth
        children.push_back(Node(depth[u], dist[u], u));
    }else if(children[depth[u]-1].cost < dist[u]){
        children[depth[u]-1] = Node(depth[u], dist[u], u);
    }
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        calculate(v, u, W[e]);
    }
}
 
void decompose(int u, int p=0){
    if(ans) return;
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);
 
    if(sz < distl) return; // ignore small paths
 
    dist[centroid] = 0;
    depth[centroid] = 0;
    build(sz); // clear segment tree
    upd(0, 0, centroid); // update centroid
    
    // find result for paths going throught this centroid
    for(int e:Adj[centroid]){
        if(ans) return;
        int v = adj(centroid, e);
        if(v == p || deleted[v]) continue;
 
        children.clear();
        calculate(v, centroid, W[e]);
 
        // query from previous subtrees
        for(Node node: children){
            int lrange = distl - node.depth, rrange = min(distr, sz) - node.depth;
            if(rrange < 0) continue;
            pair<int, int> x = get(max(lrange, 0), rrange+1);
            if(x.first + node.cost >= 0){
                ans = true;
                node_ans = {node.idx, x.second};
                return;
            }
        }
 
        // insert old subtree into segment tree
        for(Node node: children){
            upd(node.depth, node.cost, node.idx);
        }
    }
 
    deleted[centroid] = 1; // remove centroid
    for(int e:Adj[centroid]){
        int v = adj(centroid, e);
        if(v == p || deleted[v]) continue;
        decompose(v, centroid);
    }
}
 
int main() {
    int n;
    scanf("%d %d %d", &n, &distl, &distr);
    vector<int> weights;
    for(int i=1;i<n;i++){
        scanf("%d %d %d", U+i, V+i, W+i);
        weights.push_back(W[i]);
        Adj[U[i]].push_back(i);
        Adj[V[i]].push_back(i);
    }
 
    // Binary search the weights for medium
    sort(weights.begin(), weights.end());
    weights.resize(unique(weights.begin(), weights.end()) - weights.begin());
    int low = 0, high = weights.size() -1;
    // Find last i which is T in T .. T F .. F
    while(low < high){
        int mid = (low + high + 1)/2;
 
        preprocess();
        weight = weights[mid];
        decompose(1);
 
        if(ans){
            low = mid;
        }else{
            high = mid - 1;
        }
    }
    weight = weights[low];
    preprocess();
    decompose(1);
    printf("%d %d\n", node_ans.first, node_ans.second);
    return 0;
}

CF Croc Champ 2013 Round 2 E Close Vertices

You've got a weighted tree, consisting of n vertices. Each edge has a non-negative weight. The length of the path between any two vertices of the tree is the number of edges in the path. The weight of the path is the total weight of all edges it contains.

Two vertices are close if there exists a path of length at most l between them and a path of weight at most w between them. Count the number of pairs of vertices v, u (v < u), such that vertices v and u are close.

https://codeforces.com/contest/293/problem/E

Using Centroid decomposition

• We can do centroid decomposition and find the number of pairs compatible for this node at each centroid. For every element (x,y) answer the query xbound = L - x, ybound = W - y (we use centroid tree ancestor nodes).
• See count function which is key in this problem - Say we have an array tmp of pairs (a, b) It counts the number of pairs (i, j) i < j such that ai + aj <= len && bi + bj <= weight.

#include <bits/stdc++.h>

using namespace std;

const int nax = 1e5 + 10;

struct bit{
	int tree[nax];
	void add(int x, int v){
		x += 2;
		while(x < nax){
			tree[x] += v;
			x += x & -x;
		}
	}
	int sum(int x){
		x += 2; int ret = 0;
		if(x < 0) return 0;
		while(x){
			ret += tree[x];
			x -= x & -x;
		}
		return ret;
	}
} bit;

int U[nax], V[nax], W[nax];
int sub[nax];
int dist[nax], depth[nax];
bool deleted[nax];
vector<int> Adj[nax];

int len, weight;
long long ans = 0;

vector<pair<int,int>> tmp; // (depth, distance)

// number of pairs (ai, bi) & (aj, bj) such that ai + aj <= len && bi + bj <= weight
long long count(){
    sort(tmp.begin(), tmp.end(), [&](const pair<int,int> &a, const pair<int,int> &b){
		    return a.second < b.second;
    });

    int pnt = 0;
    long long ret = 0;
    for(int i=tmp.size()-1;i>=0;i--){
        while(pnt < tmp.size() && tmp[i].second + tmp[pnt].second <= weight){
            bit.add(tmp[pnt++].first, 1);
        }
        // [0, pnt) are compatible with weight of tmp[i]
        ret += bit.sum(len - tmp[i].first);
    }

    // clear fenwick tree
    while(pnt > 0){
        bit.add(tmp[--pnt].first, -1);
    }

    for(int i=0; i<tmp.size(); i++){ // each i is counted with itself
        if(tmp[i].first <= len/2 && tmp[i].second <= weight/2) ret--;
    }
    return ret/2; // each value is double counted twice
}

 
inline int adj(int u, int e){
    return U[e] ^ V[e] ^ u;
}
 
int dfs_sz(int u, int p){
    sub[u] = 1;
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        sub[u] += dfs_sz(v, u);
    }
    return sub[u];
}
 
int find_centroid(int u, int p, int sz){
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u;
}
 
vector<pair<int,int>> children, all_children;
 
void calculate(int u, int p, int edge){
    dist[u] = dist[p] + W[edge];
    depth[u] = depth[p] + 1;
    children.push_back({depth[u], dist[u]});
    for(int e:Adj[u]){
        int v = adj(u, e);
        if(v == p || deleted[v]) continue;
        calculate(v, u, e);
    }
}

void decompose(int u, int p=0){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);
 
    dist[centroid] = 0;
    depth[centroid] = 0;
    all_children.clear();
    all_children.push_back({0, 0}); // add centroid
    
    // find result for paths going throught this centroid
    for(int e:Adj[centroid]){
        int v = adj(centroid, e);
        if(v == p || deleted[v]) continue;
 
        children.clear();
        calculate(v, centroid, e);
        tmp = children;
        ans -= count(); // remove contribution of child with itself
 
        for(pair<int,int> child: children){
            all_children.push_back(child);
        }
    }
    tmp = all_children;
    ans += count();
 
    deleted[centroid] = 1; // remove centroid
    for(int e:Adj[centroid]){
        int v = adj(centroid, e);
        if(v == p || deleted[v]) continue;
        decompose(v, centroid);
    }
}

int main() {
    int n;
    scanf("%d %d %d", &n, &len, &weight);
    for(int i=2;i<=n;i++){
        U[i] = i;
        scanf("%d %d", V+i, W+i);
        Adj[U[i]].push_back(i);
        Adj[V[i]].push_back(i);
    }
    decompose(1);
    printf("%lld\n", ans);
    return 0;
}

Open Cup 2014-15 Grand Prix of Tatarsta

Problem D. LWDB, ICL’2015 - main event Russia, Kazan, 15.05.2015

You are given a tree with at most 10^5 vertices, where each edge has an integer length, and a sequence of 10^5 updates and queries. Each update tells to color all vertices in the tree that are at most the given distance from the given vertex with the given color. Each query requires you to output the current color of a given vertex.

Solution

Consider any two vertices A and B in the tree and the path connecting them, and let's find the vertex C with the smallest label on that path. It's not hard to see that the path connecting A and B lies entirely in the part that vertex C was the centroid of in the above process, and that A and B lie in different parts that appear after removing C. So our path is concatenation of two paths: from C to A, and from C to B.

Whenever we need to color all vertices B at distance at most D from the given vertex A with color X, we will group possible B's by C - the vertex with the smallest label on the path from A to B - Centroid. To find all possible C's, we just need to follow the "decomposition parent" links from A, and there are at most O(logN) such C's. For each candidate C, we will remember that all vertices in its part with distance at most D-dist(A,C) from C need to be colored with color X.

When we need to handle the second type of query, in other words when we know vertex B but not A, we can also iterate over possible candidate C's. For each C, we need to find the latest update recorded there where the distance is at least dist(B, C). After finding the latest update for each C, we just find the latest update affecting B by comparing them all, and thus learn the current color of B.

Finally, in order to find the last update for each C efficiently, we will keep the updates for each C in a stack where the distance decreases and the time increases (so the last item in the stack is always the last update, the previous item is the last update before that one that had larger distance, and so on). Finding the latest update with at least the given distance is now a matter of simple binary search.

IOI 2011

Given a weighted tree with N(1 ≤ N ≤ 200000) nodes, find the minimum number of edges in a path of length K(1 ≤ K ≤ 1000000), or return −1 if such a path does not exist. 1 ≤ length(i, j) ≤ 1000000 (integer weights)

Brute force solution

• For every node, perform DFS to find distance and number of edges to every other node.
• Time complexity: O(n^2)
• Obviously fails because N = 200000.

Centroid Decomposition

• Perform centroid decomposition to get a “tree of subtrees”
• Start at the root of the decomposition, solve the problem for each subtree as follows
  • Solve the problem for each “child tree” of the current subtree
  • Perform DFS from the centroid on the current subtree to compute the minimum edge count for paths that include the centroid
    • Two cases: centroid at the end or in the middle of path
    • Use a timestamped array of size 1000000 to keep track of which distances from centroid are possible and the minimum edge count for that distance
  • Take the minimum of the above two
• Time complexity: O(n log n)

YATP - NAIPC 2016

This is Yet Another Tree Problem. You are given a tree, where every node has a penalty and every edge has a weight. The cost of a simple path between any two nodes is the sum of the weights of the edges in the path, plus the product of the penalties of the endpoint nodes. Note that a path can have 0 edges, and the cost of such a path is simply the square of the penalty of the node.

For each node, compute the smallest cost of any path starting at that node. The final answer is the sum of all of these minimum costs.

source: https://open.kattis.com/problems/yatp, https://codeforces.com/gym/101002

Using centroid decomposition, Dynamic Convex hull trick

• Consider the node(say x) with least penalty value, what will be the smallest cost of any path starting at this node? The cost will be (penalty[x])², because choosing any other vertex would lead to higher cost.
• From the above oberservation, for any node with penality y, the smallest cost will be to a node with penality < y.
• Therefore, we can sort the N nodes in increasing order of penalty and perform the following operations:
  • Activate x_i: Activate the node x_i
  • Query x_i: Find the optimal node y_i, from the sert of already activated nodes [x₁, x₂, ..., x_i] s.t dist(x_i, y_i) + pen[x_i]*pen[y_i] is minimzed.
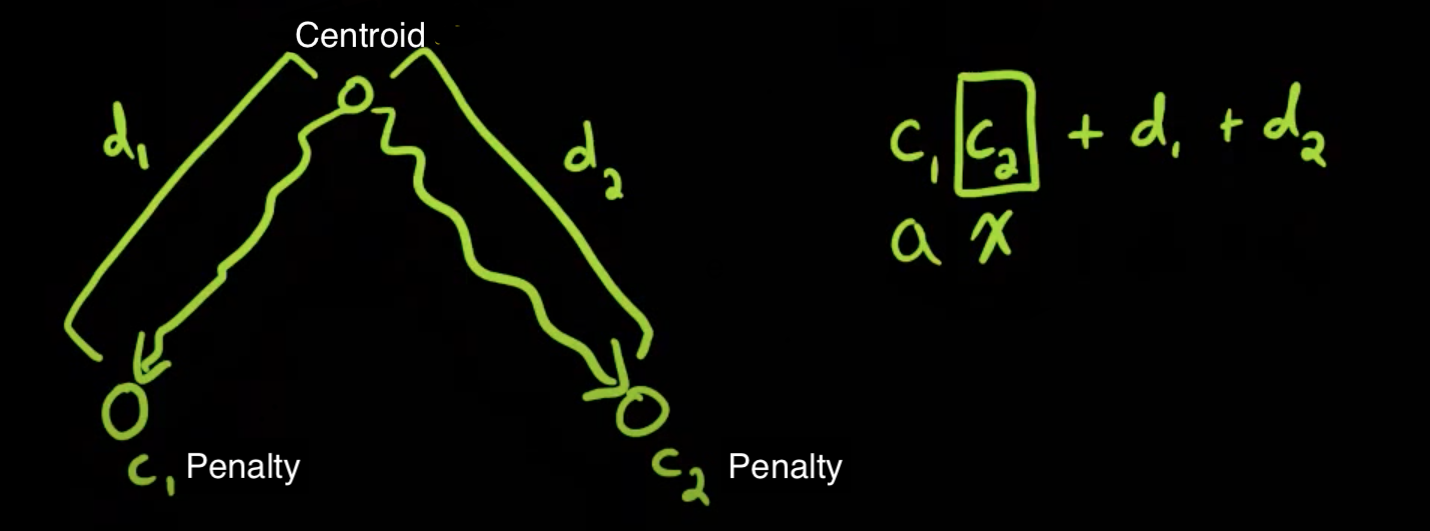
• Note that dist(x_i, y_i) = dist(x_i, c) + dist(c, y_i) where c is lca(x_i, y_i) in the centroid tree.
• If we have a DS that can support the following operations, then we can store (m = penality[x], c = dist(centroid, x)) in the DS and find the smallest cost by using eval x. To achieve this we can use Dynamic Convex Hull Trick(CHT)
  • Insert a line y = mx + c i.e, insert (m, c) in the DS
  • Eval x: Get min(m_i * x + c) for all inserted lines i
• For activating a node x, insert (penality[x], dist(centroid, x)) in Dynamic CHT of all ancestor of x in centroid tree.
• To find the smallest cost for x, perform an eval query for penality[x] at all ancestors of x.
• Since we are asked for minimum, we don't need to worry about the contribution of the centroid to it's parent. This will not work if the question asks for maximum.

const int nax = 2e5 + 10;
const int LG = 20;

#define LL long long
const LL is_query = -(1LL << 62);
struct Line {
  LL m, b;
  mutable function<const Line*()> succ;
  bool operator<(const Line& rhs) const {
    if (rhs.b != is_query) return m > rhs.m;
    const Line* s = succ();
    if (!s) return 0;
    return s->b - b < (m - s->m) * rhs.m;
  }
};
struct HullDynamic : public multiset<Line> {
  bool bad(iterator y) {  // maintains lower hull for min
    auto z = next(y);
    if (y == begin()) {
      if (z == end()) return 0;
      return y->m == z->m && y->b >= z->b;
    }
    auto x = prev(y);
    if (z == end()) return y->m == x->m && y->b >= x->b;
    return (x->b - y->b) * (z->m - y->m) >= (y->b - z->b) * (y->m - x->m);
  }
  void insert_line(LL m, LL b) {
    auto y = insert({m, b});
    y->succ = [=] { return next(y) == end() ? 0 : &*next(y); };
    if (bad(y)) {
      erase(y);
      return;
    }
    while (next(y) != end() && bad(next(y))) erase(next(y));
    while (y != begin() && bad(prev(y))) erase(prev(y));
  }
  LL eval(LL x) {
    auto l = *lower_bound((Line){x, is_query});
    return l.m * x + l.b;
  }
};

vector<int> Adj[nax];
int U[nax], V[nax], W[nax];
bool deleted[nax];
int sub[nax], par[nax], level[nax], penalty[nax];
ll dist[LG][nax];
HullDynamic CHT[nax];

// other end of edge e
int nxt(int u, int e){
    return U[e] ^ V[e] ^ u;
}

int dfs_sz(int u, int p){
    sub[u] = 1;
    for(int e:Adj[u]){
        int v = nxt(u, e);
        if(v==p || deleted[v]) continue;
        sub[u] += dfs_sz(v, u);
    }
    return sub[u];
}

int find_centroid(int u, int p, int sz){
    for(int e:Adj[u]){
        int v = nxt(u, e);
        if(v==p || deleted[v]) continue;
        if(sub[v] > sz/2) return find_centroid(v, u, sz);
    }
    return u;
}

void calculate(int u, int p, int lvl){
    for(int e:Adj[u]){
        int v = nxt(u, e);
        if(v==p || deleted[v]) continue;
        dist[lvl][v] = dist[lvl][u] + W[e];
        calculate(v, u, lvl);
    }
}

void decompose(int u, int p = 0){
    int sz = dfs_sz(u, p);
    int centroid = find_centroid(u, p, sz);

    level[centroid] = level[p] + 1; // level of centroid starts from 1
    par[centroid] = p;

    deleted[centroid] = 1;
    calculate(centroid, p, level[centroid]);

    for(int e:Adj[centroid]){
        int v = nxt(centroid, e);
        if(v==p || deleted[v]) continue;
        decompose(v, centroid);
    }
}

void activate(int u){
    int x = u;
    while(x){
        CHT[x].insert_line(penalty[u], dist[level[x]][u]);
        x = par[x];
    }
}

ll query(int u){
    ll ans = 1e18;
    int x = u;
    while(x){
        ans = min(ans, CHT[x].eval(penalty[u]) + dist[level[x]][u]);
        x = par[x];
    }
    return ans;
}

int main() {
    int n;
    scanf("%d", &n);
    vector<pair<int,int>> P;
    for(int i=1;i<=n;i++){
        int p;
        scanf("%d", &p);
        penalty[i] = p;
        P.push_back({p, i});
    }
    for(int i=1;i<n;i++){
        scanf("%d %d %d", U+i, V+i, W+i);
        Adj[U[i]].push_back(i);
        Adj[V[i]].push_back(i);
    }
    decompose(1);
    LL ans = 0;
    sort(P.begin(), P.end());
    for(int i=0;i<n;i++){
        activate(P[i].second);
        ans += query(P[i].second);
    }
    printf("%lld\n", ans);
    return 0;
}

757G — Can Bash Save the Day? CodeCraft 17

https://codeforces.com/contest/757/problem/G

Simpler question: Given a weighted tree, initially all the nodes of the given tree are inactive. We need to support the following operations fast:

• Query v : Report the sum of distances of all active nodes from node v in the given tree.
• Activate v : Mark node v to be an active node.

Centroid Decomposition

For any such questions, we should think about the following:

• What information do we need to maintain to answer the query efficiently?
• How would the update impact the information we have maintained?

At each centroid vertex, we will store the sum of distances to all activates nodes in the centroid subtree. We will need to store some more information to make sure that we don't count some values more than once.

Let us store the following information:

• Let sum[i] deonote the sum of distances to all activated nodes for the centroid i in its corresponding part.
• Let contribution[i] deonote contribution of all activated nodes in the subtree of i to sum[par[i]] in centroid tree. What is this subtree at i contributing to it's parents.
• let cnt[i] deonote the number of activated nodes in the subtree of i in the centroid tree.
• For each update, to activate a node u, we move up to all the ancestors x of u in the centroid tree and update their sum[x] += dist(x,y);, contribution[x] += dist(par[x], u); and cnt[x] += 1;
• For each query on u, we compute sum[u] + (sum[par[x]] - contribution[x] + (cnt[par[x]] - cnt[x]) * dist(par[x], u)) for all ancestors x of u.

Original Problem: Given a weighted tree and a sequence a_1, a_2, ..., a_n (permutation of 1 .. n). We need to answer Q queries of the form:

• Query l, r, v: Report Sum(dist(a_i, v)) for l ≤ i ≤ r
• Update x: Swap(a_x, a_{x+1}) in the given input sequence.

Using Persistent Centroid Decomposition

Solution Idea for query:

• Each query of the form (L, R, v) can be divided into two queries of the form (1, R, v) - (1, L-1, v). Hence it is sufficient if we can support the following query: (i, v): Report the answer to query (1, i, v).
• To answer a single query of the form (i, v) we can think of it as what is the sum of distance of all active nodes from v, if we consider the first i nodes to be active.
• Hence initially if we can preprocess the tree such that we activate nodes from 1 to n and after each update, store a copy of the centroid tree, then for each query (i, v) we can lookup the centroid tree corresponding to i, which would have the first i nodes activated, and query for node v in O(log N) time by looking at it's ancestors.
• To store a copy of the centroid tree for each i, we need to make it persistent.

Persistent Centroid Tree : Key Ideas

• Important thing to note is that single update in the centroid tree affects only the ancestors of the node in the tree.
• Since height of the centroid tree is O(log N), each update affects only O(log N) other nodes in the centroid tree.
• The idea is very similar to that of a persistent segment tree BUT unlike segtree, here *each node of the centroid tree can have arbitrarily many children and hence simply creating a new copy of the affected nodes would not work because linking them to the children of old copy would take O(number of children) for each affected node and this number could be as large as N, hence it could take O(N) time in total!

Binarizing the Input Tree

• To overcome the issue, we convert the given tree T into an equivalent binary tree T' by adding extra dummy nodes such that degree of each node in the transformed tree T' is  ≤ 3, and the number of dummy nodes added is bounded by O(N).
• The dummy nodes are added such that the structure of the tree is preserved and weights of the edges added are set to 0.
• To do this, consider a node x with degree d > 3 and let c1, c2...cd be it's adjacent nodes. Add a new node y and change the edges as follows :
• Delete the edges (x - c3), (x - c4) ... (x - cd) and add the edge (x - y) such that degree of node x reduces to 3 from d.
• Add edges (y - c3), (y - c4) ... (y - cd) such that degree of node y is d - 1. Recursively call the procedure on node y.
• Since degree of node y is d - 1 instead of original degree d of node x, it can be proved that we need to add at most O(N) new nodes before degree of each node in the tree is  ≤ 3.

We need to binarize the original tree and not centroid tree. If we binarize the cetroid tree, then height of centroid tree would increase, may not be be O(log N).

Conclusion Hence we perform centroid decomposition of this transformed tree T'. The centroid tree formed would have the following properties.

The height of the centroid tree is O(logN)

Each node in the centroid tree has ≤ 3 children.

Now we can easily make this tree persistent by path-copying approach.

To handle the updates,

• Way-1 : Observe that swapping A[i] and A[i + 1] would affect only the i'th persistent centroid tree, which can be rebuilt from the tree of i - 1 by a single update query. In this approach, for each update we add new nodes. See author's code below for more details.
• Way-2 : First we go down to the lca of A[x] and A[x + 1] in the x'th persistent tree, updating the values as we go. Now, let cl be the child of lca which is an ancestor of A[x], and let cr be the child which is an ancestor of A[x + 1]. Now, we replace cr of x'th persistent tree with cr of (x + 1)'th persistent tree. Similarly, we replace cl of x + 1'th persistent tree with cl of x'th persistent tree. So now A[x + 1] is active in x'th persistent tree and both A[x] and A[x + 1] are active in (x + 1)'th persistent tree.To deactivate A[x] in x'th persistent tree we replace cl of x'th persistent tree with cl of (x - 1)'th persistent tree. Hence in this approach we do not need to create new O(log N) nodes for each update. See testers's code below for more details.

//Tanuj Khattar
#include<bits/stdc++.h>

using namespace std;

typedef pair<int,int>   II;
typedef vector< II >      VII;
typedef vector<int>     VI;
typedef vector< VI > 	VVI;
typedef long long int 	LL;

#define PB push_back
#define MP make_pair
#define F first
#define S second
#define SZ(a) (int)(a.size())
#define ALL(a) a.begin(),a.end()
#define SET(a,b) memset(a,b,sizeof(a))

#define si(n) scanf("%d",&n)
#define dout(n) printf("%d\n",n)
#define sll(n) scanf("%lld",&n)
#define lldout(n) printf("%lld\n",n)
#define fast_io ios_base::sync_with_stdio(false);cin.tie(NULL)

#define TRACE

#ifdef TRACE
#define trace(...) __f(#__VA_ARGS__, __VA_ARGS__)
template <typename Arg1>
void __f(const char* name, Arg1&& arg1){
  cerr << name << " : " << arg1 << std::endl;
}
template <typename Arg1, typename... Args>
void __f(const char* names, Arg1&& arg1, Args&&... args){
  const char* comma = strchr(names + 1, ',');cerr.write(names, comma - names) << " : " << arg1<<" | ";__f(comma+1, args...);
}
#else
#define trace(...)
#endif

//FILE *fin = freopen("in","r",stdin);
//FILE *fout = freopen("out","w",stdout);
const int MAXN = int(2e5)+10;
const int MAXQ = int(2e5)+10;
const int N = 2*MAXN;
const int M = 2*N;
int A[N]; //the permutation given
int last[N],prv[M],nxt[M],to[M],deg[N],W[M],root[N];
namespace tree{
  int sz,edge,vis[N];
  void addEdge(int u,int v,int w = 0){
    prv[edge] = last[u];W[edge] = w;
    if(last[u]!=-1)nxt[last[u]] = edge;
    last[u] = edge;
    to[edge] = v;
    edge++;
  }
  void addEdge1(int u,int v,int e){
    prv[e] = last[u];nxt[e] = -1;
    if(last[u]!=-1)nxt[last[u]] = e;
    last[u] = e;
    to[e] = v;
  }
  void deleteEdge(int u,int e){
    if(nxt[e]!=-1)prv[nxt[e]] = prv[e];
    if(prv[e]!=-1)nxt[prv[e]] = nxt[e];
    if(last[u] == e) last[u] = prv[e];
  }
  void changeEdge(int u,int v,vector<int> edges){
    //assert(SZ(edges) == 3);assert(deg[u] > 3);
    sort(ALL(edges));reverse(ALL(edges));
    for(auto e : edges)
      deleteEdge(u,e);
    last[v] = last[u];
    last[u] = -1;
    for(auto e : edges)
      addEdge1(u,to[e],e);
  }
  void pre(){
    SET(last,-1);SET(nxt,-1);
    SET(prv,-1);SET(to,-1);
  }
  //binarize the give tree.should be called from a leaf node.
  void binarize(int u,int p,int edge){
    vis[u]=1;
    if(deg[u] > 3){
      addEdge(u,++sz);
      deg[sz] = deg[u] - 1;
      set<int> temp;temp.insert(edge^1);
      int e = last[u];
      while(SZ(temp) < 3){
        temp.insert(e);
        e = prv[e];
      }
      changeEdge(u,sz,vector<int>(temp.begin(),temp.end()));
      deg[u] = 3;
      addEdge(sz,u);
    }
    for(int e = last[u];e >= 0; e = prv[e]){
      if(!vis[to[e]])
        binarize(to[e],u,e);
      else to[e] = p;
    }
  }
}
namespace Centroid{
  const int LOGN = 19;
  const int MAXC = N + (MAXN + MAXQ)*LOGN;
  int sub[N],nn,done[M],C[MAXC][3],L[N],R[N],idx[N],len[N],T,cnt[MAXC],lvl,IDX[MAXC];
  LL sum[MAXC],cntbn[MAXC],dist[LOGN][N];
  void dfs1(int u,int p){
    sub[u]=1;nn++;
    for(int e = last[u];e >= 0; e = prv[e]){
      int w = to[e];
      if(w!=p && !done[e])
        dfs1(w,u),sub[u]+=sub[w];
    }
  }
  int dfs2(int u,int p){
    for(int e = last[u];e >= 0; e = prv[e]){
      if(done[e])continue;int w = to[e];
      if(w!=p && sub[w]>nn/2)
        return dfs2(w,u);
    }return u;
  }
  void dfs(int u,int p){
    for(int e = last[u];e >= 0; e = prv[e]){
      if(done[e] || to[e]==p)continue;
      dist[lvl][to[e]] = dist[lvl][u] + W[e];
      dfs(to[e],u);
    }
  }
  int decompose(int root,int p,int l = 0){
    nn=0;dfs1(root,root);
    root=dfs2(root,root);
    lvl = l;dfs(root,root);
    idx[root] = ++T;
    int id = idx[root];IDX[T] = T;
    L[id] = T;
    for(int e = last[root];e >= 0;e = prv[e]){
      if(done[e])continue;
      assert(!done[e^1]);
      done[e]=done[e^1]=1;
      int c = decompose(to[e],root,l+1);
      assert(len[id] < 3);
      C[id][len[id]++] = idx[c];
    }
    R[id] = T;
    return root;
  }
  int update(int x,int id,int lvl=0){
    int ID = ++T;
    cnt[ID] = cnt[id] + 1;
    sum[ID] = sum[id] + dist[lvl][x];
    IDX[ID] = IDX[id];
    for(int i=0;i<len[IDX[id]];i++)
      if(L[IDX[C[id][i]]] <= idx[x] && idx[x] <= R[IDX[C[id][i]]]){
        C[ID][i] = update(x,C[id][i],lvl+1);
        cntbn[C[ID][i]] = cntbn[C[id][i]] + dist[lvl][x];
      }
      else C[ID][i] = C[id][i];
    return ID;
  }
  LL query(int x,int id,int lvl=0){
    LL ret = sum[id];
    for(int i=0;i<len[IDX[id]];i++)
      if(L[IDX[C[id][i]]] <= idx[x] && idx[x] <= R[IDX[C[id][i]]])
        ret += query(x,C[id][i],lvl+1) - cntbn[C[id][i]] + (cnt[id] - cnt[C[id][i]])*dist[lvl][x];
    return ret;
  }
}
void binarize(int n){
  int root = -1;
  for(int i=1;i<=n;i++)
    if(deg[i] == 1)
      root = i;
  tree::binarize(root,root,-1);
}
int main()
{
  tree::pre();
  int n,q;
  si(n);si(q);
  tree::sz = n;
  for(int i=1;i<=n;i++)si(A[i]);
  for(int i=1;i<n;i++){
    int u,v,w;
    si(u);si(v);si(w);
    tree::addEdge(u,v,w);
    tree::addEdge(v,u,w);
    deg[u]++;deg[v]++;
  }
  //binarize the given tree
  binarize(n);
  //build the centroid tree.
  Centroid::decompose(1,-1);
  root[0] = 1;
  //make it persistent and handle the queries.
  for(int i=1;i<=n;i++)
    root[i] = Centroid::update(A[i],root[i-1]);
  const int MOD = (1 << 30);
  LL ans = 0;
  while(q--){
    int t;si(t);
    if(t==1){
      int l,r,v;
      si(l);si(r);si(v);
      l = l ^ ans;
      r = r ^ ans;
      v = v ^ ans;
      ans = Centroid::query(v,root[r])-Centroid::query(v,root[l-1]);
      lldout(ans);
      ans = ans % MOD;
    }
    else{
      int x;si(x);x = x ^ ans;
      root[x] = Centroid::update(A[x+1],root[x-1]);
      swap(A[x],A[x+1]);
    }
  }
  return 0;
}

Another approach: https://codeforces.com/blog/entry/49743?#comment-337109, http://codeforces.com/contest/757/submission/23772311

Difference between HLD and CD

• If we want to compute something on paths then we use HLD
• If we want to compute something on an area surrounding node, we use CD. For example: Say we are given node u and distance D and we want to compute something on nodes v such that dist(u, v) ≤ D, something around node u.

TODO - https://codeforces.com/blog/entry/52492?locale=en

Implementation: https://codeforces.com/contest/321/submission/3973635, https://codeforces.com/contest/321/submission/45791725, https://usaco.guide/plat/centroid?lang=cpp, https://codeforces.com/contest/1303/submission/76216413, neal https://codeforces.com/contest/1303/submission/70880989, https://github.com/SuprDewd/CompetitiveProgramming/blob/5b326ad153f52d46a84f3d670f035af59a3ec016/code/graph/centroid_decomposition.cpp

https://discuss.codechef.com/t/cheftraf-editorial/16813

TODO: Solve this problem https://codeforces.com/contest/1174/problem/F, https://discuss.codechef.com/t/trdst-editorial/21978 and https://www.codechef.com/problems/BTREE and https://codeforces.com/contest/566/problem/C

TODO: https://codeforces.com/contest/833/problem/D

REF:

• https://medium.com/carpanese/an-illustrated-introduction-to-centroid-decomposition-8c1989d53308
• https://robert1003.github.io/2020/01/16/centroid-decomposition.html
• https://threadsiiithyderabad.quora.com/Centroid-Decomposition-of-a-Tree
• https://petr-mitrichev.blogspot.com/2015/03/this-week-in-competitive-programming_22.html
• https://codeforces.com/blog/entry/10533#comment-159119