Notes

// from kmjp
// source: https://kmjp.hatenablog.jp/entry/2021/03/29/0900

ll mo=1000000007;
ll comb(ll N_, ll C_) {
	const int NUM_=400001;
	static ll fact[NUM_+1],factr[NUM_+1],inv[NUM_+1];
	if (fact[0]==0) {
		inv[1]=fact[0]=factr[0]=1;
		for (int i=2;i<=NUM_;++i) inv[i] = inv[mo % i] * (mo - mo / i) % mo;
		for (int i=1;i<=NUM_;++i) fact[i]=fact[i-1]*i%mo, factr[i]=factr[i-1]*inv[i]%mo;
	}
	if(C_<0 || C_>N_) return 0;
	return factr[C_]*fact[N_]%mo*factr[N_-C_]%mo;
}

// Something noteworthy is you have to calculate binomial coefficients modulo 3, 
// but you can't do it naively since n! = 0 mod3, ∀ n ≥ 3. 
// To get around this, keep track of the power of 3 in 𝑛! (say 𝑝) and the value of 𝑛! without any powers of 3.
// Or use Lucas theorem

// Lucas theorem for mod = 3
int C[3][3];

int getC(int n, int k) {
	if (k < 0 || k > n) return 0;
	int ans = 1;
	while(n > 0) {
		int x = n % 3;
		int y = k % 3;
		n /= 3;
		k /= 3;
		ans = (ans * C[x][y]) % 3;
	}
	return ans;
}

// inside main
    for (int i = 0; i < 3; i++)
		C[i][0] = C[i][i] = 1;
	for (int i = 1; i < 3; i++)
		for (int j = 1; j < i; j++)
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % 3;


// binary exponentiation
ll modpow(ll a, ll n) {
	ll r=1;
	while(n) r=r*((n%2)?a:1)%mo,a=a*a%mo,n>>=1;
	return r;
}
 
ll comb(int P_,int Q_) {
	if(P_<0 || Q_<0 || Q_>P_) return 0;
	ll p=1,q=1;
	Q_=min(Q_,P_-Q_);
	for(int i=1;i<=Q_;i++) p=p*P_%mo, q=q*i%mo,P_--;
	
	return p*modpow(q,mo-2)%mo;
}
 
void solve() {
	int i,j,k,l,r,x,y; string s;
	
	cin>>N>>M>>K;
	
	ll ret=0;
	FOR(i,N) {
		ll d=1LL*i*(i+1)/2%mo;
		d=d*M%mo*M%mo;
		ret+=d;
	}
	FOR(i,M) {
		ll d=1LL*i*(i+1)/2%mo;
		d=d*N%mo*N%mo;
		ret+=d;
	}
	
	cout<<ret%mo*comb(N*M-2,K-2)%mo<<endl;
}

TODO: https://codeforces.com/contest/1536/problem/F

Enumerative combinatorics

Catalan numbers

The Catalan numbers are a remarkable sequence of numbers that “solve” a number of seemingly unrelated counting problems.

Triangulation of polygon: A convex (n+2)-gon can be split into n triangles by n-1 non-intersecting diagonals. The number of different ways of splitting is given by catalan number Cn.

Proof: Given (n+2)-gon, say we consider the base of the polygon and number vertices from 1 to n. Suppose that the third vertex of the base triangle is k, the green polygon is k+1-gon and the red polygon is n+k-2-gon, then we get the following recurrence relation.
Casheir Problem: Cn is the number of ways to form a "mountain range" with n upstrokes and n downstrokes that all stay above a horizontal line. The mountain range interpretation is that the mountains will never go below the horizon. For n = 3 Cn = 5.
Say in a country we only have 2 coin denominations 5 and 10. Now suppose that we have 2n people in a line waiting to buy a movie ticket, n of them are having 5 rupees and the other n are having 10 rupees and the cashier has no change. How many different ways are possible such that ticket seller is always able to satisfy all the people. If we consider 5 as +1 and 10 as -1 then for the people in the line, the prefix sum should always be >= 0. If we consider 5 as moving 1 unit in x direction and 10 and moving 1 unit in y direction. We should never touch the line y = x + 1.

The number of invalid paths can be calculated Andre's reflection principle. Andre's Reflection Principle: A path is invalid if it touches or crosses the line y = x + 1. In any case it touches the line the first time at let's say 𝑃. Now, we reflect the first part of the path from 𝐴=(0,0) to 𝑃 at the line y = x + 1 getting a path from A′=(−1,1). So the total valid paths = [All paths from (0, 0) to (n, n)] - [All paths from (-1, 1) to (n, n)]. [All paths from (0, 0) to (n, n)] = [number of ways of arranging n A's and n B's = (2n choose n)]

Similarly if cashier initally has k 5 rupee denominations then the diagonal moves up k units and we can use reflection priniciple.

Bertrand's ballot problem is the question: "In an election where candidate A receives p votes and candidate B receives q votes with p > q, what is the probability that A will be strictly ahead of B throughout the count?" The answer is (p - q)/(p + q). The number of favourable ways (p+q-1 choose p-1) - (p+q-1 choose p). Proof: First vote should always go to candidate A, now we are left with (p-1) A's votes and q B's votes and now ties are allowed, so by reflection trick we get (p+q-1 choose p-1) - (p+q-1 choose p). If ties are allowed in the original problem then the answer would be (p+q choose q) - (p+q choose q-1).

Application: CHNBGMT https://discuss.codechef.com/t/chnbgmt-editorial/12438, https://www.spoj.com/problems/FUNPROB/, Lots of Combinations Problem B Petr Mitrichev Contest 10 https://codeforces.com/gym/100110

https://atcoder.jp/contests/abc167/tasks/abc167_e

ABC 209 Problem C - Not Equal

You are given a sequence C of N integers. Find the number of sequences A of N integers satisfying all of the following conditions. 1 ≤ Aᵢ ≤ Cᵢ ( 1 ≤ i ≤ N ) Aᵢ ≠ Aⱼ ( 1 ≤ i < j ≤ N ) Since the count may be enormous, print it modulo (10⁹ + 7).

Solution: Sort Cᵢ in increasing order and Now for each of the index i we have max(0, Cᵢ - (i-1)) choices to choose the element. We can prove this because, after determining the first i − 1 elements A₁ , A₂ , … , the candidates for Aᵢ are 1 , 2 , … Cᵢ , except for A₁ , A₂ , … Aᵢ − 1 (which are all pairwise distinct and between 1 and Cᵢ , inclusive); namely there are (Cᵢ − i + 1) candidates. If however any i satisfies Cᵢ − i + 1 < 0, then the answer is 0 .

https://atcoder.jp/contests/abc209/tasks/abc209_c

Leetcode Paiting a grid with 3 different colors

Painting a m * n grid with three different colors such that no two adjacent cells have same color, Here 1 <= m <= 5 & 1 <= n <= 1000 since m is very small we can create a graph where each node denotes a column (c1, c2, c3, c4, c5) and count the number of columns compatible with this using dynamic programming.

https://leetcode.com/problems/painting-a-grid-with-three-different-colors/

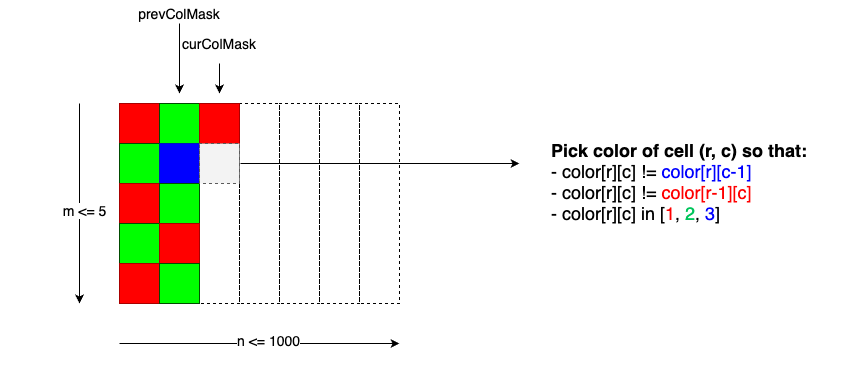
class Solution {
public:
    int memo[1000][1024] = {};
    int m, n, MOD = 1e9 + 7;
    int colorTheGrid(int m, int n) {
        this->m = m; this->n = n;
        return dp(0, 0, 0, 0);
    }
    int dp(int c, int prevColMask, int r, int curColMask) {
        if (c == n) return 1; // Found a valid way
        if (r == 0 && memo[c][prevColMask]) return memo[c][prevColMask];
        if (r == m) return dp(c + 1, curColMask, 0, 0);
        int ans = 0;
        for (int i = 1; i <= 3; ++i) // Try colors i in [1=RED, 2=GREEN, 3=BLUE]
            if (getColor(prevColMask, r) != i && (r == 0 || getColor(curColMask, r-1) != i))
                ans = (ans + dp(c, prevColMask, r + 1, setColor(curColMask, r, i))) % MOD;
        if (r == 0) memo[c][prevColMask] = ans;
        return ans;
    }
    int getColor(int mask, int pos) { // Get color of the `mask` at `pos`, use 2 bits to store a color
        return (mask >> (2 * pos)) & 3;
    }
    int setColor(int mask, int pos, int color) { // Set `color` to the `mask` at `pos`, use 2 bits to store a color
        return mask | (color << (2 * pos));
    }
};

Probability of derangements is 1/e https://math.stackexchange.com/questions/399500/why-is-the-derangement-probability-so-close-to-frac1e

https://ico-official.com/assets/media/archive/ico-booklet-2020-en.pdf

Number of Integer solutions for the equation x1 + x2 + ... + xr = n and x >= 0 is C(n+r-1, r-1).

Proof: We can assume we want to arrange (r-1) + symbols and (n) 1's so it is (n-r+1)!/(n! (r-1)!).

If we want solutions such that x > 0, then it is arranging (r-1) + symbols into gaps of n 1's that is 1 x 1 x 1 .. x 1 we need to choose (r-1) x positions out of the available (n-1) positions and hence we have C(n-1, r-1)

REF: https://math.stackexchange.com/questions/919676/the-number-of-integer-solutions-of-equations

Problem based on this: https://atcoder.jp/contests/abc132/tasks/abc132_d

Colorful Hats 2

N people are standing in a queue, numbered 1 , 2 , 3 , . . . , N from front to back. Each person wears a hat, which is red, blue, or green.

The person numbered i says: "In front of me, exactly Ai people are wearing hats with the same color as mine."

Assuming that all these statements are correct, find the number of possible combinations of colors of the N people's hats. Since the count can be enormous, compute it modulo 1000000007 .

Solution

#include <iostream>
#include <string>
using namespace std;
#pragma warning (disable: 4996)

int N, A[1 << 18], C[3];
long long sum = 1;

int main() {
	cin >> N;
	for (int i = 1; i <= N; i++) cin >> A[i];

	for (int i = 1; i <= N; i++) {
		long long cnt = 0, id = -1;
		if (A[i] == C[0]) { cnt++; id = 0; }
		if (A[i] == C[1]) { cnt++; id = 1; }
		if (A[i] == C[2]) { cnt++; id = 2; }
		if (id == -1) {
			cout << "0" << endl;
			return 0;
		}
		sum *= cnt; C[id]++;
		sum %= 1000000007;
	}
	cout << sum << endl;
	return 0;
}