Notes
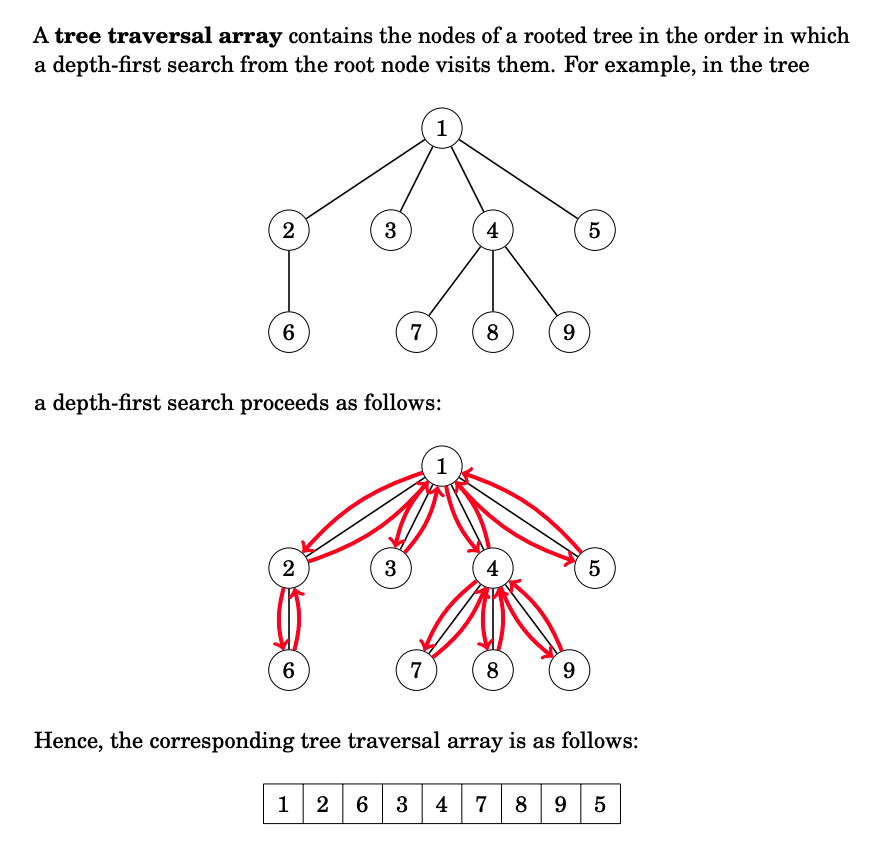
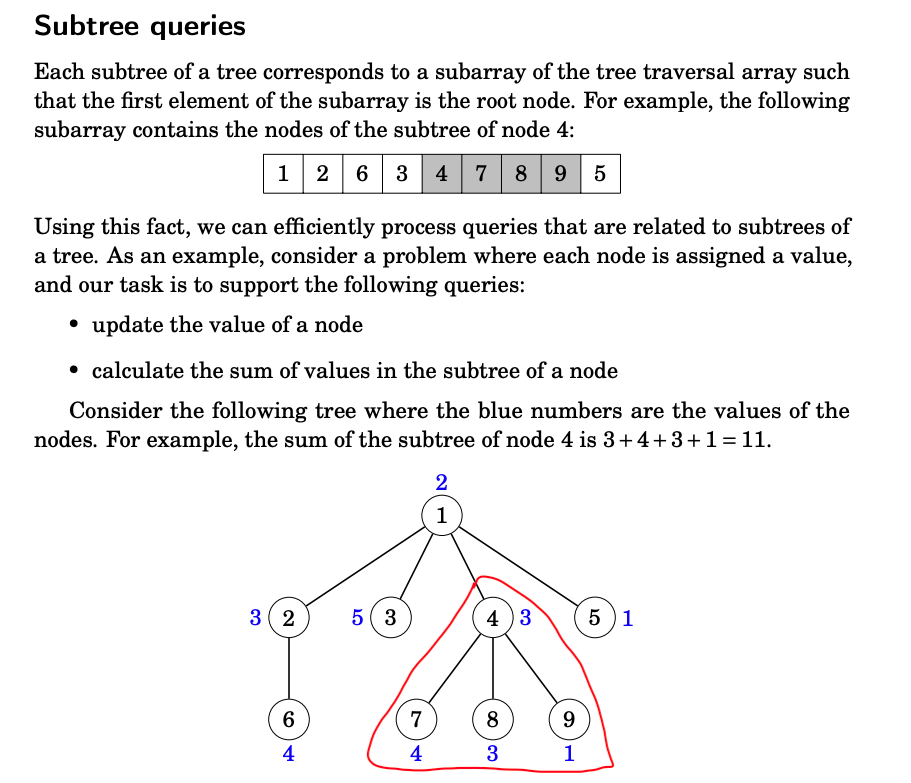

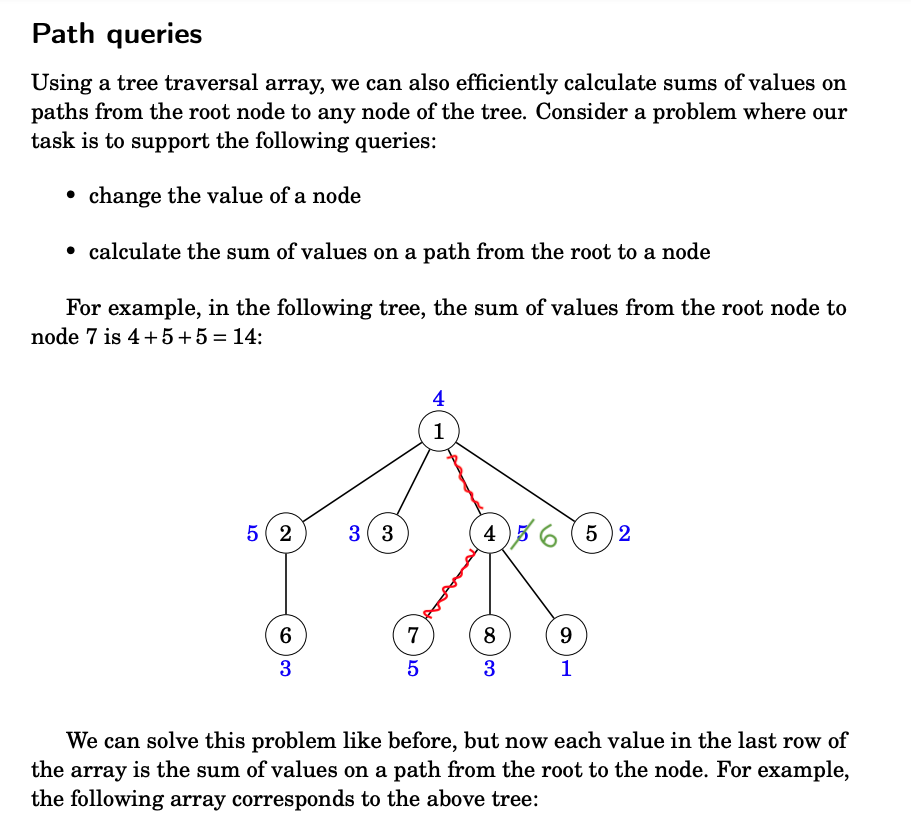

source: Competitive Programmer's Handbook - CSES
Euler Tour trees
Euler tour tree (ETT) is a method for representing a rooted undirected tree as a number sequence. There are several common ways to build this representation.
1
/ \
2 5
/ \
3 4
[1-2] [2-3] [3-2] [2-4] [4-2] [2-1] [1-5] [5-1] - Edges in order of DFS
1
/ \
2 5
/ \
3 4
1 2 3 3 4 4 2 5 5 1 - Vertex is added to the array twice, once during start of DFS and again while end of DFS
1
/ \
2 5
/ \
3 4
1 2 3 2 4 2 1 5 1 - Each vertex is added every time when we visit it
Further all ETT's are stored in a Cartesian tree (treap) unless other explicitly stated. first(v) and last(v) are positions of first and last occurrence of vertex v in the array (in 2nd and 3rd cases).
So, how these representation can be used?
First, you should notice that a subtree is always mapped to a segment. Thus you can solve subtree queries via segment queries. E.g. if you want to add values to nodes and find subtree sum, you just make a BIT on a 2nd type tour. add(v, x) becomes add(first(v), x) in BIT, and get_sum(v) becomes get_sum(first(v), last(v)) in BIT. There is also a trick to compute sum on path: add(v, x) becomes add(first(v), x), add(last(v), - x) in BIT, and get_sum_on_path_from_root(v) is get_sum(0, first(v)) (you can check that it works using pencil and paper).
You can also use ETT for finding LCA. Use the 3rd type. Make an additional array h, where h[i] = height(v[i]). Then lca(u, v) = v[argmin(first(u), first(v)) in h]. Why? Because LCA(u, v) is a highest vertex which is between u and v in DFS traverse order. Sometimes I prefer this method to binary lifting because it proved to be faster and consumes linear memory.
The fact that a subtree is maps to a segment gives us some more benefits. With the first and third approach you can reroot the tree simply rotating the array. You may avoid some pain in the neck with the third approach if you do not store last number for the root (thus vertex v will have exactly deg(v) occurrences). You also can perform link-cut operations simply cutting the segment from the array. It is done quite straightforward when you store edges, and with vertices you should carefully deal with duplicating of the subtree's former ancestor.
Queries on Trees:
Path Query and Update Problems
- Path Query: Given two nodes x, y - compute some function f(x, y) that depends on the path between nodes x & y.
- Eg: sum, min, max, number of distinct elements etc.
- Point Update: Change the value for any one edge/node in the tree.
- Path Range Update: Change the value of all nodes/edges on a path.
- Eg: Add x to all nodes in a path, take mod x for all nodes in a path etc.
Subtree Query and Update Problems
- Subtree Query: Given a node x - compute some function f(x) that depends on values of nodes/edges in the subtree of x
- Eg: sum, min, max, number of distinct elements etc.
- Point Update: Change the value of any one edge / node in the tree
- Subtree Range Update: Change the value of all nodes/edges in the subtree of a node x.
- Eg: Add "val" to all all nodes in the subtree of node x etc.
How to support Updates & Queries on a Tree?
- Step-1: Find a way to "Linaerize" the tree into an array.
- Heavy Light Decomposition: Any path between (x, y) can be represented as concatenation of at-most logN different [L,R] ranges in the linearised array.
- Euler Tour Traversal: Any subtree of a node x corresponds to a single range [L, R] in the linearised array.
- Step-2: Use one of the "standard" techniques to solve the update/query problem on the linearised tree.
- Eg: Segment Trees, Square Root Decomposition etc.
Euler Tour Technique(ETT)
Way-1: Insert every node twice
- Insert every node/edge in the euler tour array whenever you enter and exit the node.
- Thereforce, every node/edge of the tree will occur twice in the euler tour array - at indices
start[x]/in[x]andend[x]/out[x]for a given node/edge x.
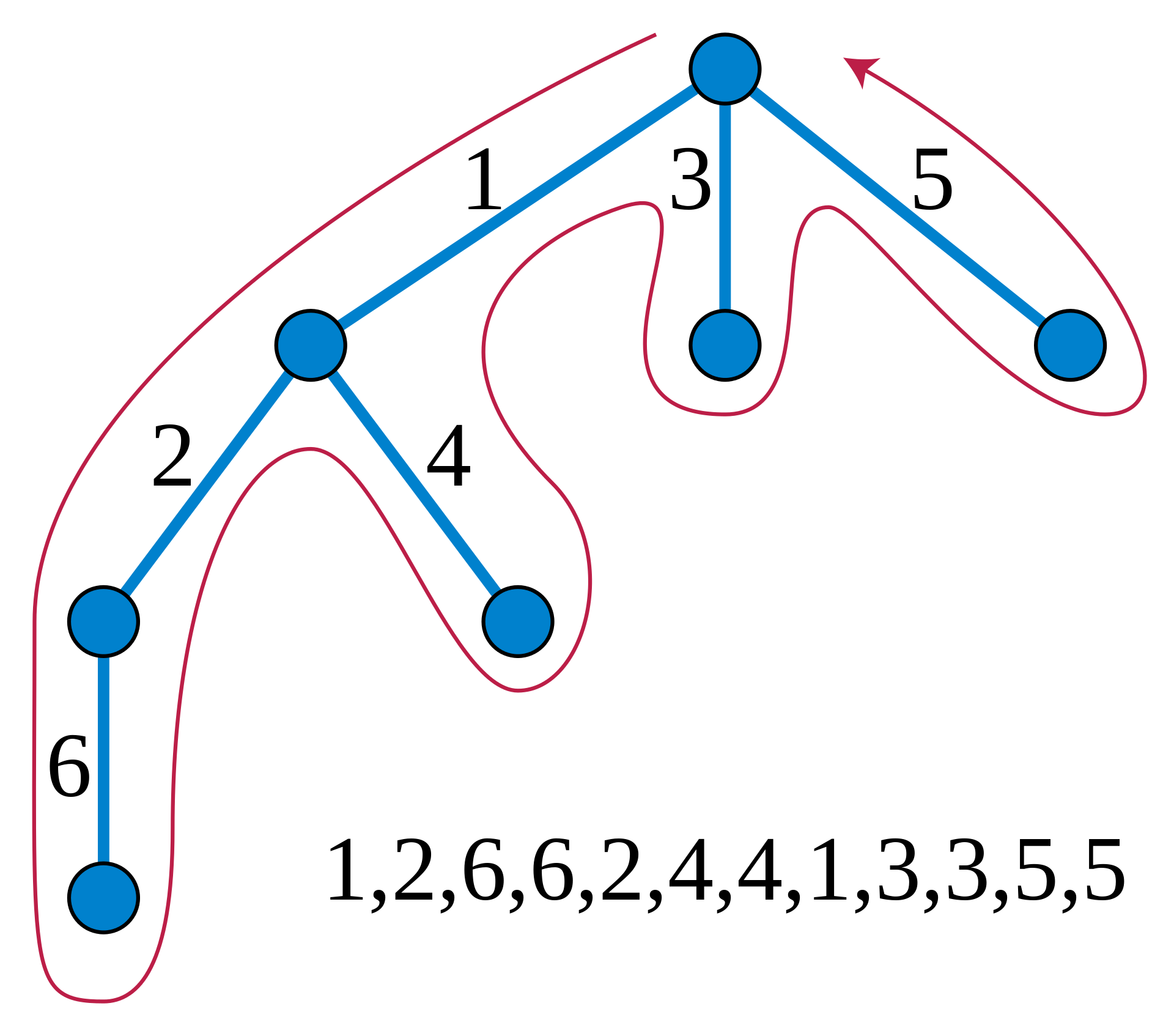
- A subtree of node x is represented by the continous range
[start[x], end[x]] - A path between the two nodes A & B contain nodes which occur exactly once in the continous range
[end[A], start[B]]-- Useful for applying MO's on Trees where we can ignore an element y if it occurs twice in the range[L, R]. For example in case of Addition of path, When we see the node for the first time, we can add the element to sum and, when we see it the second time we can subtract thus nullifying the element which occurs twice in the range[L, R]. Read more
Way-2: Insert every node only once
- Insert every node/edge in the euler tour array whenever you enter the node and increment the timer
- start[x] = timer at which you enter the node x.
- end[x] = timer at which you exit the node x.
- All nodes in subtree of x occur exact once in the range
[start[x], end[x]]
Steps to support subtree updates/queries
- Build the Euler tour array for the given tree by doing a DFS
- Maintain a data structure on the Euler Tour array that supports range queries/updates
- For any query/update on all nodes in the subtree of node x, process it as a query/update on range
[start[x], end[x]]in the linearised array.
Simultaneously maintaining Euler Tour & HLD
- What if you wish to support path and subtree updates & queries together?
- tl;dr Simply add start[x], end[x] computation to HLD DFS.
- HLD is also a Way-2 Euler Tour Ordering
- In HLD, the "order" in which we call DFS on children is decided by subtree sizes.
- But once that is done, we "add our node to the array" and "increase the timer" whenever we enter a node for the first time.
- Therefore we can simply maintain the start[x] and end[x] times for every node
x, similar to Way-2 of Euler Tour Technique. - Now any subtree
xwill be present as a linear range [start[x], end[x]] - Any path from vertex A to chainHead[chainNo[A]] will be present as a linaer range[start[chainHead[chainNo[A]]], start[A]] - exactly same as the usual HLD
void dfs_sz(int v = 0) {
sz[v] = 1;
for(auto &u: g[v]) {
dfs_sz(u);
sz[v] += sz[u];
if(sz[u] > sz[g[v][0]]) {
swap(u, g[v][0]);
}
}
}
void dfs_hld(int v = 0) {
in[v] = t++;
for(auto u: g[v]) {
nxt[u] = (u == g[v][0] ? nxt[v] : u);
dfs_hld(u);
}
out[v] = t;
}
source: https://codeforces.com/blog/entry/53170
Hackerrank: Subtrees and Paths
https://www.hackerrank.com/challenges/subtrees-and-paths/problem
You can now support simultaneous Queries and Updates of the form
- Range subtree Update: Add val to all nodes in the subtree of x
- Range Path Update: Add val to all nodes on path from node x to y
- Range Subtree Query: Return sum of all nodes in the subtree of x
- Range Path Query: Return sum of all nodes on the path from node x to y
In O(log²N) via HLD + Euler Tour + Segment Tree 🚀
USACO guide implementation
If we can preprocess a rooted tree such that every subtree corresponds to a contiguous range on an array, we can do updates and range queries on it!
After running dfs(), each range [st[i], en[i]] contains all ranges [st[j], en[j]] for each j in the subtree of i. Also, en[i]-st[i]+1 is equal to the subtree size of i.
const int MX = 2e5+5;
vector<int> adj[MX];
int timer = 0, st[MX], en[MX];
void dfs(int node, int parent) {
st[node] = timer++;
for (int i : adj[node]) {
if (i != parent) {
dfs(i, node);
}
}
en[node] = timer-1;
}
Applications
Subtree sum
Your task is to process following types of queries:
- change the value of node s to x
- calculate the sum of values in the subtree of node s
https://cses.fi/problemset/task/1137/
Solution
Linearize the tree using ETT and create segment tree on top of it. Each subtree of a tree corresponds to a subarray of the tree traversal array such
that the first element of the subarray is the root node. Subtree of node x is store from [st[x], en[x]].
To answer the queries efficiently, it suffices to store the values of the nodes in a binary indexed or segment tree. After this, we can both update a value and calculate the sum of values in O(logn) time.
/**
* Description: 1D point update, range query where \texttt{comb} is
* any associative operation. If $N=2^p$ then \texttt{seg[1]==query(0,N-1)}.
* Time: O(\log N)
* Source:
* http://codeforces.com/blog/entry/18051
* KACTL
* Verification: SPOJ Fenwick
*/
template<class T> struct Seg { // comb(ID,b) = b
const T ID{}; T comb(T a, T b) { return a+b; }
int n; vector<T> seg;
void init(int _n) { // upd, query also work if n = _n
for (n = 1; n < _n; ) n *= 2;
seg.assign(2*n,ID); }
void pull(int p) { seg[p] = comb(seg[2*p],seg[2*p+1]); }
void upd(int p, T val) { // set val at position p
seg[p += n] = val; for (p /= 2; p; p /= 2) pull(p); }
T query(int l, int r) { // any associative op on interval [l, r]
T ra = ID, rb = ID;
for (l += n, r += n+1; l < r; l /= 2, r /= 2) {
if (l&1) ra = comb(ra,seg[l++]);
if (r&1) rb = comb(seg[--r],rb);
}
return comb(ra,rb);
}
int first_at_least(int lo, int val, int ind, int l, int r) { // if seg stores max across range
if (r < lo || val > seg[ind]) return -1;
if (l == r) return l;
int m = (l+r)/2;
int res = first_at_least(lo,val,2*ind,l,m); if (res != -1) return res;
return first_at_least(lo,val,2*ind+1,m+1,r);
}
};
const int nax = 2e5 + 10;
int timer = 0;
vector<int> Adj[nax];
int st[nax], en[nax]; // start and end time
// Euler tour tree
void dfs(int u, int p){
st[u] = timer++;
for(int v:Adj[u])
if(v != p) dfs(v, u);
en[u] = timer-1;
}
int val[nax];
int main() {
int n, q;
scanf("%d %d", &n, &q);
Seg<long long> tree;
tree.init(n);
for(int i=0;i<n;i++){
scanf("%d", val+i);
}
for(int i=0;i<n-1;i++){
int u, v;
scanf("%d %d", &u, &v);
u--; v--;
Adj[u].push_back(v);
Adj[v].push_back(u);
}
dfs(0, -1);
for(int i=0;i<n;i++){
tree.upd(st[i], val[i]);
}
while(q--){
int type;
scanf("%d", &type);
if(type==1){
int s, x;
scanf("%d %d", &s, &x);
tree.upd(st[s-1], x);
}else{
int s; scanf("%d", &s);
printf("%lld\n", tree.query(st[s-1], en[s-1]));
}
}
return 0;
}
Root to Path Queries
Your task is to process following types of queries:
- change the value of node s to x
- calculate the sum of values on the path from the root to node s
Solution using segment tree
When the value of a node increases by x, the sums of all nodes in its subtree increase by x.
To support both the operations, we should be able to increase all values in a range and retrieve a single value. This can be done in O(logn) time using a binary indexed or segment tree
template<class T, int SZ> struct LazySeg {
static_assert((SZ & (SZ-1)) == 0); // SZ must be power of 2
const T ID = 0; T comb(T a, T b) { return a+b; }
T seg[2*SZ], lazy[2*SZ];
LazySeg() { for(int i=0; i<2*SZ; i++) seg[i] = lazy[i] = ID; }
void push(int ind, int L, int R) { // modify values for current node
seg[ind] += (R-L+1)*lazy[ind]; // dependent on operation
if (L != R) for(int i=0; i<2;i++) lazy[2*ind+i] += lazy[ind]; // prop to children
lazy[ind] = 0;
} // recalc values for current node
void pull(int ind) { seg[ind] = comb(seg[2*ind],seg[2*ind+1]); }
void build() { for(int i=SZ-1; i>=1; i--) pull(i); }
void upd(int lo,int hi,T inc,int ind=1,int L=0, int R=SZ-1) {
push(ind,L,R); if (hi < L || R < lo) return;
if (lo <= L && R <= hi) {
lazy[ind] = inc; push(ind,L,R); return; }
int M = (L+R)/2; upd(lo,hi,inc,2*ind,L,M);
upd(lo,hi,inc,2*ind+1,M+1,R); pull(ind);
}
T query(int lo, int hi, int ind=1, int L=0, int R=SZ-1) {
push(ind,L,R); if (lo > R || L > hi) return ID;
if (lo <= L && R <= hi) return seg[ind];
int M = (L+R)/2;
return comb(query(lo,hi,2*ind,L,M),query(lo,hi,2*ind+1,M+1,R));
}
};
const int nax = 2e5 + 10;
vector<int> adj[nax];
int timer = 0;
int st[nax], en[nax], par[nax];
void dfs(int u, int p){
par[u] = p;
st[u] = timer++;
for(int v: adj[u]){
if(v == p) continue;
dfs(v, u);
}
en[u] = timer - 1;
}
LazySeg<long long, (1<<19) > tree;
int main() {
int n, q; scanf("%d %d", &n, &q);
vector<int> V(n);
for(int i=0;i<n;i++){
scanf("%d", &V[i]);
}
for(int i=0;i<n-1;i++){
int a, b; scanf("%d %d", &a, &b);
a--; b--;
adj[a].push_back(b);
adj[b].push_back(a);
}
dfs(0, -1);
for(int i=0;i<n;i++){
tree.upd(st[i], en[i], V[i]);
}
while(q--){
int type; scanf("%d", &type);
if(type == 1){
// change the node value to x
int s; long long x; scanf("%d %lld", &s, &x); s--;
long long prev = tree.query(st[s], st[s]);
int p = par[s];
if(p != -1) prev -= tree.query(st[p], st[p]);
tree.upd(st[s], en[s], 1ll*x - prev);
}else{
int x; scanf("%d", &x); x--;
printf("%lld\n", tree.query(st[x], st[x]));
}
}
return 0;
}
Notice that when we update a node with value A[s] to x, the root-to-node sum for each node in its subtree increases by the difference x-A[s]. Using ETT,
this is equivalent to a range update.
We can use a Fenwick tree which supports range increment/decrements and point queries in O(log N) time.
When implementing your solution, recall that incrementing a range [a, b] with a Fenwick tree corresponds to the operations upd(a, x) and upd(b+1, -x)
Fenwick tree CPP implementation
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using vi = vector<int>;
#define pb push_back
#define all(x) begin(x), end(x)
#define sz(x) (int) (x).size()
using pi = pair<int,int>;
#define f first
#define s second
#define mp make_pair
/**
* Author: Lukas Polacek
* Date: 2009-10-30
* License: CC0
* Source: folklore/TopCoder
* Description: Computes partial sums a[0] + a[1] + ... + a[pos - 1],
* and updates single elements a[i],
* taking the difference between the old and new value.
* Time: Both operations are $O(\log N)$.
* Status: Stress-tested
*/
struct FT {
vector<ll> s;
FT(int n) : s(n) {}
void update(int pos, ll dif) { // a[pos] += dif
for (; pos < sz(s); pos |= pos + 1) s[pos] += dif;
}
ll query(int pos) { // sum of values in [0, pos)
ll res = 0;
for (; pos > 0; pos &= pos - 1) res += s[pos-1];
return res;
}
};
const int mx = 2e5+1;
vi adj[mx];
int A[mx], st[mx], en[mx];
int timer = 0;
FT ft(mx+1);
void dfs(int x, int p) { // euler tour
st[x] = timer++;
for(const int &e : adj[x]) if(e != p) dfs(e, x);
en[x] = timer-1;
}
int main() {
int n, q;
cin >> n >> q;
for(int i = 1; i <= n; i++) cin >> A[i];
for(int i = 0; i < n-1; i++) {
int a, b; cin >> a >> b;
adj[a].pb(b);
adj[b].pb(a);
}
dfs(1, 0);
for(int i = 1; i <= n; i++) {
ft.update(st[i], A[i]);
ft.update(en[i]+1, -A[i]);
}
for(int i = 0; i < q; i++) {
int type, s; cin >> type >> s;
if(type == 1) {
int x; cin >> x;
ft.update(st[s], x-A[s]);
ft.update(en[s]+1, -(x-A[s])); // nullify from [en+1, ...]
A[s] = x;
} else {
cout << ft.query(st[s]+1) << '\n';
}
}
}
source: https://usaco.guide/problems/cses-1138-path-queries/solution
Euler Tour Magic
Euler tour magic. Consider following problem: you have a tree and there are lots of queries of kind
- add number on subtree of some vertex
- calculate sum on the path between some vertices.
HLD? Damn, no! Let's consider two euler tours: in first we write the vertex when we enter it, in second we write it when we exit from it. We can see that difference between prefixes including subtree of v from first and second tours will exactly form vertices from v to the root. Thus problem is reduced to adding number on segment and calculating sum on prefixes. Worth mentioning that there are alternative approach which is to keep in each vertex linear function from its height and update such function in all v's children, but it is hard to make this approach more general.
source: Trick 12 from adamant https://codeforces.com/blog/entry/48417
Consider the following tree,
1
/ | \
2 5 6
/ \
3 4
If we visit the nodes in the order [1,2,3,4,5,6] the euler tour we build is [1,2,3,3,4,4,2,5,5,6,6,1]. Notice each number appears twice, one to represent entering and one for exiting (backtracking). Updating a node can be done by adding v in the start position and subtracting v from the end position of a node. Updating subtrees can be done with some range update ideas/keeping track of frequency of starts/ends in some interval. Querying can be done by finding the sum of numbers up to the first position the number shows up.
[1,2,3,3,4,4,2,5,5,6,6,1] - Order in which nodes are visited and exited.
[1,2,3,0,4,0,0,5,0,6,0,0] - Values of each node are stored in the positions of their first appearance.
[0,0,0,3,0,4,2,0,5,0,6,1] - Values of each node are stored in the positions of their second appearance.
Then, if you wanted to get the sums of the numbers from node 3 to the root, you would simply take two range sum queries:
[1,2,3, 0,4,0,0,5,0,6,0,0] - Query from first segment tree
[0,0,0, 3,0,4,2,0,5,0,6,1] - Query from second segment tree
and subtract the first query from the second query, giving us 3+2+1!
In terms of prefixes, the sum of vertex from 1-2-4 is [1,2,3,0,4 ,0,0,5,0,6,0,0] - [0,0,0,3,0 ,4,2,0,5,0,6,1] = 1 + 2 + 4!
Alternate Approach
If we create a array with nodes when we enter but not when we exit, then we can query subtrees and update a node in O(logn) with BIT/Segment Tree.
The way to query paths is not much different, instead of creating an event only when you enter, you must also create an event for when you exit the node (2 copies). This is because you want to ignore nodes not in the path: nodes with event that end before current one begins in the euler tour. Why are these not in path? Because an exit/ending event indicates backtracking, and if it backtracked from some node A before going into the current node B, node A can't possibly be on path from root to B.
Consider 2 copies for a single node in the Euler tour, one for entry and one for exit. When you want to add a value v to the subtree, maintain a fenwick tree, and do +=v on in[node] and -=v on out[node]. Path sum query can be broken down to sum from root to any node. For the root to node sum query, just return prefix sum of in[node] from BIT.
Now why does this work? Think about a single subtree update and then querying for prefix sum. Let's assume you updated subtree of node x with value v. Now, if you query for some node which is not in the subtree of x, the answer will be 0, either in[node]<in[x] then it's obviously 0, or in[node]>out[x] then in[x] and out[x] cancel out, so it's still 0. For the nodes inside the subtree of x, in[x]<in[node]<out[x]. So, they'll all return the value v. So effectively we've updated the subtree of x with value v.
source: https://codeforces.com/blog/entry/63020
Another type of Euler Tour that's useful is one where you add in the node every time its stack frame reappears in the DFS. For the given tree, the Tour would look like: [1,2,3,2,4,2,1,5,1,6,1]
Then, one nice thing about this tour is that you can compute LCA using it, by creating a segment tree with the nodes in this order, and stores pairs of {depth, node}. So, the segment tree would be created over the array
[{0, 1}, {1, 2}, {2, 3}, {1, 2}, {2, 4}, {1, 2}, {0, 1}, {1, 5}, {0, 1}, {1, 6}, {0, 1}]
If you create a Range Min Query over this, and want to find, say, the LCA of nodes 3 and 4, then you just take a Range Min Query of the indices that they appear at:
[{0, 1}, {1, 2}, {2, 3}, {1, 2}, {2, 4}, {1, 2}, {0, 1}, {1, 5}, {0, 1}, {1, 6}, {0, 1}]
And the lowest {depth, node} pair we find is {1, 2}, meaning that node 2 is the LCA.
source: https://codeforces.com/blog/entry/63020?#comment-469803
Checkout https://codeforces.com/blog/entry/78564
TODO
- TODO: https://usaco.guide/gold/tree-euler?lang=cpp
- TODO: https://codeforces.com/gym/102694
- TODO: Important property of ETT https://codeforces.com/contest/1328/problem/E and https://www.codechef.com/JULY21C/problems/KPATHQRY