Notes

Game Theory

Formal study of mathematical games. The ultimate goal of game theory is usually to solve a game; that is, to determine the nature of an optimal strategy for each player, and the outcome of such a strategy.

State

Determinism

Availability of information

Partiality

Play convention

If, in addition to being deterministic, impartial, and guaranteed to end in a finite number of moves, a game is also normal play, it can be analyzed using the Sprague-Grundy theorem. We shall denote such games as Nim-like.

source: http://wcipeg.com/wiki/Game_theory

N-positions and P-positions

In a two-player, deterministic(no chance moves), impartial game which is guaranteed to end(win-or-lose outcome) in a finite number of moves, an N-position is a configuration such that the next player(and so it is a win for the Next player—hence the “N”) to make a move can force victory, and a P-position is a configuration such that the previous player who moved can force victory.

In a normal-play game, a configuration in which no further moves are possible is a P-position, since the player who is supposed to move next cannot do so and loses; in a misère-play game, it is an N-position, since the player who moved last made the last move and hence lost.

Consider a configuration C of such a game and the configurations C_1, C_2, C_3, ... reachable from it.

In summary,

The problem Nukit from the 2008 Canadian Computing Competition describes a game which is clearly two-player, deterministic, impartial, and guaranteed to end in a finite number of moves. Because of these properties we may analyze it with N-positions and P-positions.

Basic problem

A simple example is the following game, played by two players who take turns moving. At the beginning there are n coins. When it is a player’s turn he can take away 1, 3 or 4 coins. The player who takes the last one away is declared the winner (in other words, the player who can not make a move is the loser). The question is: For what n will the first player win if they both play optimally?

Positions have the following properties:

These properties could be used to create a simple recursive algorithm WL-Algorithm:

boolean isWinning(position pos) {
    moves[] = possible positions to which I can move from the position pos;
    for (all x in moves)
        if (!isWinning(x)) return true;
    return false;
}

No cycles in the state transitions – Can solve the problem bottom-up (DP)

It can be seen that whether a position is winning or losing depends only on the last k positions, where k is the maximum number of coins we can take away. While there are only 2^k possible values for the sequences of the length k, our sequence will become periodic.

You can use this observation to solve SRM 330: LongLongNim

The way to solve the game is pretty easy. Since there are no ties and the game is always finite, we know that for each n either there is a winning strategy for the first player or there is a winning strategy for the second player. We'll call ``n a winning (W) state if the player in turn wins when `n` coins are left and losing `(L)` otherwise. Of course all `n` that are less than the minimum element in moves are `L`. Then, each `n` is `W` if and only if there exists an element `m` in moves that is less than or equal to `n` and such that `n-m` is `L` (this means, there is a valid play that leaves a losing state to your rival). This leads to a straightforward implementation which gets the fact calculated for every n in `O(maxN*k)` where `k` is the number of elements on moves (the `k` factor could even be eliminated by doing bit tricks). Since `maxN` is insanely big, we need something even better.

The first thing to notice in the constraints is the 22 as the maximum move. This was a big clue to the solution. As you can see from the previous paragraph, each n only depends on the previous states n-m with m in moves. Since the maximum m is 22, we can say n depends in the state of n-1, ...,n-22. This can be represented as a 22 character long string of W's and L's (or as a binary number). Not only n depend only on that 22 character long string, the entire behavior from that moment on depends only on those 22 characters, because the string in which n+1 depends is simply appending the state of n at the end and removing the first character (that becomes unnecessary, because is more than 22 away from n>+1). Altogether, this means that after at most 2^22 numbers there's an indentifiable cycle, which can be used to calculate the rest of the moves without doing all the process. See Petr's code for a clear implementation.

public class LongLongNim {
    public int numberOfWins(int maxN, int[] moves) {
        int mask = (1 << 22) - 1;
        int res = -1;
        Dictionary < int, int > last = new Dictionary < int, int > ();
        List < int > r = new List < int > ();
        for (int i = 0; i <= maxN; ++i) {
            mask <<= 1; // mask = mask * 2, left shift
            ++res;
            foreach(int j in moves)
            if ((mask & (1 << j)) == 0) // atleast one losing position
            {
                ++mask; // set 0-th bit to 1
                --res;
                break;
            }
            mask &= (1 << 22) - 1; // only consider the last 22 bits
            if (last.ContainsKey(mask)) {
                int pLength = i - last[mask]; // cycle length
                int cnt = (maxN - i) / pLength;
                i += cnt * pLength;
                res += cnt * (res - r[last[mask]]);
            }
            last[mask] = i;
            r.Add(res);
        }
        return res;
    }
}

Proving that our strategy works

To prove that our strategy works for a problem we need to satisfy these three conditions

Example problem

Say we are given N piles, each pile is having Ai stones. In a move we need to divide all piles having > 1 stones into two piles. For example say we have (3, 4, 5, 1) piles then in a move we can divide them into ({1, 2}, {2, 2}, {1,4}, {1}) piles. Now we are having (1, 2, 2, 2, 1, 4, 1) piles.

Hence the final position will contains piles of size only 1.

Solution: The problem only depends on the pile with largest number of stones. If the largest pile is having 2^k - 1 stones then it is losing position otherwise it is winning position.

Proof:

THE GAME OF NIM

The rules of the game are as follows:

Suppose that there are two players A, B and three heaps with 3, 4 and 5 coins respectively. Here is how game could develop if A moves first:

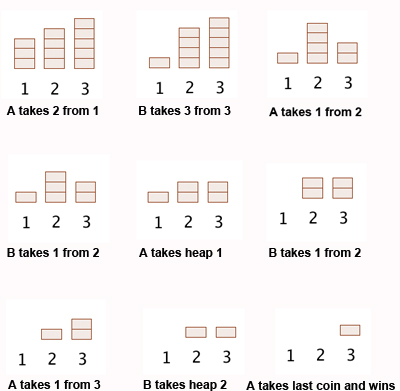
Analysis

Bouton’s Theorem: The position (x, y, z) is a P-position if and only if x ⊕ y ⊕ z = 0

Let n1, n2, n3, ... nk be the size of the piles. It is a losing position for the player whose turn it is if and only if n1 xor n2 xor ... xor nk = 0.

Why does it work?

Dynamic pile problem

The game of 'static' one-pile nim is well understood. These are called subtraction games. A pile of n counters and a constant k are given. Two players alternately take from 1 up to k counters from the pile. The winner is the last player to remove a counter.

Dynaic one-pile nim, A move in a game is an ordered pair of positions (N,x) —> (N — k, f(k)), where 1 < k < min{N, x}. problem where f(k) = k https://csacademy.com/contest/round-64/task/limited-moves/statement/.

An infinite increasing sequence B = (b0 = 1, b1, b2, ...) of positive integers is called an infinite g-base if for each k > 0, b_{k+1} ≤ bk.

Th: Suppose the dynamic one-pile nim game with initial position (N,x) and move function/satisfying f(n+1) - f(n) ≥ 1 is given, and the g-base Bf is infinite. Also, let N = b1 + b2 + ... + bk be the stable representation of N in Bf, where b1 < b2 < ... < bk. Then the first player can win if x > b1 and the second player can win if x < b1.

Proof in Research Paper: Holshouser DYNAMIC ONE-PILE NIM

Solution:

In order to find the winning strategy we can run a dynamic programming for smaller values of NN and check which are the winning states; it turns out the first player can win for all N that are not a power of 2. However, we still need to:

It helps to consider the binary representation of N. The strategy for the first player is to choose a power of 2 that removes the first significant bit in N's representation. In the next turn, whatever he does, the second player will increase the number of bits of 1 in the representation.

If n is odd then we win by removing 1. So no one will move to odd n and the game will be always on even numbers. But now we can divide all numbers by 2 and repeat our argument. It is easy to see that this strategy is exactly 'remove last 1-bit'. https://codeforces.com/blog/entry/57075?#comment-407190

Another variation of nim

Say not only removing stones like in normal nim game, In a move a player can choose to add stones to some pile. What would be the winning position? If players keep on adding the stones then the game doesn't end in finite moves. So let's say a player can add stones atmost 10 times. What would be the winning position? Suprisingly the 0 xor sum is still a losing position because: Say a person is in losing in position and add some stones to a pile, then the other player can remove the exact number of stones the other player has added nullifying the addition move. Thus it is similar to nim game.

Grundy numbers (Nimbers)

Let G be an impartial game. The Grundy number of a position P in G is

Ever finite 2-person impartial games with perfect information can be converted into an equivalent Nim game using the Grundy Numbers.

For one pile games: Let G be an impartial game, and let g be its Grundy function. Then P is a winning position for player I whenever g(P) > 0, and P is a winning position for player II whenever g(P) = 0.

Here are Grundy numbers for (1, 3, 4)-NUM for upto 21 stones.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
0 1 0 1 2 3 2 0 1 0  1  2  3  2  0  1  0  1  2  3  2  0

The sequence is periodic with repeating pattern 0, 1, 0, 1, 2, 3, 2. Using this pattern we have the following

Here are the Grundy numbers for (2, 4, 7)-NIM (where each player can remove 2, 4, or 7 stones) up to 21 stones.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
L L W W W W L W W L  W  W  L  W  W  L  W  W  L  W  W  L
0 0 1 1 2 2 0 3 1 0  2  1  0  2  1  0  2  1  0  2  1  0

The sequence is eventually periodic with repeating pattern 1, 0, 2. Notice that it has an initial segment of length 8, as compared to length 4 when we looked only at win/loss information (W, W, L) pattern.

Composite games - Grundy numbers

Composite games are combination of multiple simple games.

Example game: Consider N x N chessboard with K knights on it. Unlike a knight in a traditional game of chess, these can move only as shown in the picture below (so the sum of coordinates is decreased in every move). There can be more than one knight on the same square at the same time. Two players take turns moving and, when it is a player’s, turn he chooses one of the knights and moves it. A player who is not able to make a move is declared the loser.

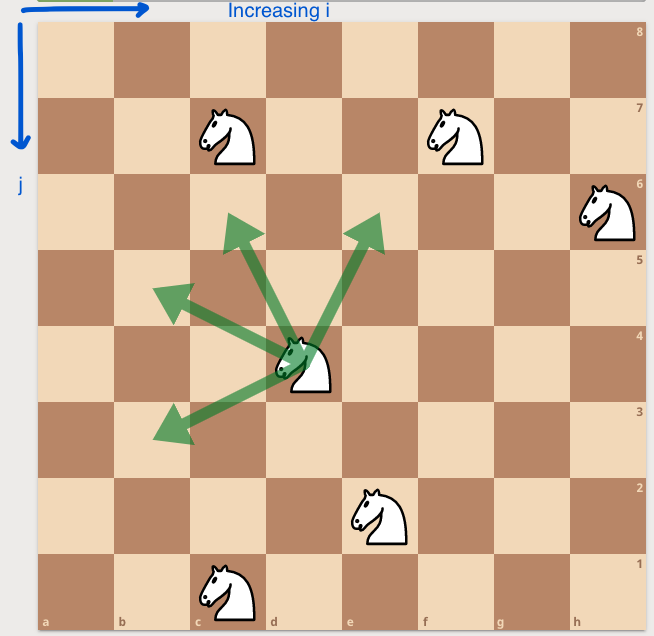
This is the same as if we had K chessboards with exactly one knight on every chessboard. This is the ordinary sum of K games and it can be solved by using the grundy numbers. We assign grundy number to every subgame according to which size of the pile in the Game of Nim it is equivalent to. When we know how to play Nim we will be able to play this game as well.

int grundyNumber(position pos) {
    moves[] = possible positions to which we can move from pos
    set s;
    for(all x in moves) insert into s grundyNumber(x);
    //return the smallest non-negative integer not in the set s;    
    int ret = 0;
    while(s.contains(ret)) ret++;
    return ret;
}

The following table shows grundy numbers for an 8 x 8 board:

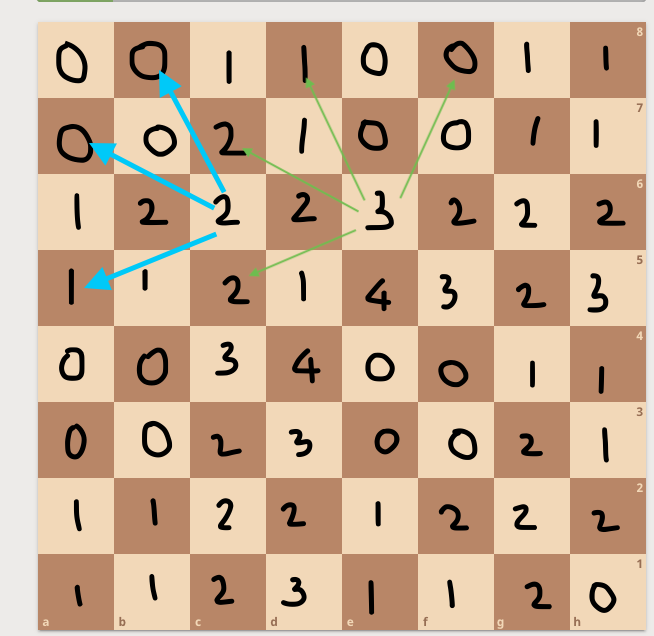
We could try to solve the original problem with our WL-Algorithm, but it would time out because of the large number of possible positions.

A better approach is to compute grundy numbers for an N x N chessboard in O(n^2) time and then xor these K (one for every horse) values. If their xor is 0 then we are in a losing position, otherwise we are in a winning position.

Why is the pile of Nim equivalent to the subgame if its size is equal to the grundy number of that subgame?

Generalization

Assume that we have games with the following properties:

Let’s call the games satisfying these properties as solvable games. For such games, there is a theory to find the winning strategy. This involves the Sprague–Grundy theorem, which reduces every such game to a game of Nim.

Sprague-Grundy theorem reduces the state of every such game to a single Nim pile of a certain size. This pile size is called the nimber/Grundy number of the state. The theorem then essentially states that the state of a game is a winning/losing position iff the corresponding Nim pile is a winning/losing state.

source: https://letuskode.blogspot.com/2014/08/grundy-numbers.html

Sum of games

If some games are played in parallel in a "super" game (i.e. upon his turn, a player may decide to move in any of the currently active game; when there is no valid move in any of the games, the player looses), then this "super" game is called the SUM of all the parallel "small" games.

If the "small" game have Grundy Numbers {G1, G2, ..., Gn} then the "super" game has Grundy Number G = {G1 xor G2 xor ... xor Gn}.

Now, the game of Nim can be considered as the sum many of single pile Nim games. Since, we know that each single piles' grundy number is equal to the number of stones in that pile, the overall grundy number is simply their xor. This is consistent with what we have done earlier.

Now, lets consider some simple games and find their Grundy Numbers.

Game 1:

Unlike Nim, here you can only remove 1,2 or 3 stones from a choosen pile (there is only one pile as of now). Now, , , , , , and so on, i.e. . Grundy numbers wasn't really necessary to figure out who wins in a single pile. But in case of multiple piles, it really helps to find out the grundy number of each pile and take the xor.

Game 2:

Consider an infinite grid, a coin is placed at , in each turn, a player can move the coin along decreasing co-ordinate or decreasing co-ordinate by as many steps as he desires with the only restriction being that neither nor become negative at any point. This is basically a 2-pile Nim game with pile heights and respectively!

Only key thing to remember while applying the sum of games is that the games should be independent of each other, and the player in a move will choose one of the game and play a move in it.

TODO: https://atcoder.jp/contests/abc206/tasks/abc206_f

Problem: https://atcoder.jp/contests/abc195/tasks/abc195_e

Solution:

Let us consider if Takahashi is possible to win after the N − 1 rounds. Let us regard T as a decimal number and r be the remainder by 7 .

Also, we identify SN with the corresponding digit.

If XN is T, then Takahashi will win if either 10r or 10r + SN is a multiple of 7 .

If XN is A, then Takahashi will win if both 10r and 10r + SN are multiples of 7 .

As you can see, we can define the following DP, in the reversed order.

dp[i]=The set of integers r that satisfies the following condition, where Condition: if the remainder of T divided by 7 is r after the ith round end, Takahashi will win

The initial state is dp[N] = { 0 }.

The transitions are

dp[i−1] = { r | ( 10r mod 7 ) ∈ dp[i]  or ( 10r + Sᵢ mod 7 ) ∈ dp[i]}  if Xᵢ is `T`, 

dp[i−1] = { r | ( 10r mod 7 ) ∈ dp[i] and ( 10r + Sᵢ mod 7 ) ∈ dp[i]}  if Xᵢ is `A`,

If 0 ∈ dp[0] at last, Takahashi wins; otherwise, Aoki wins. The time complexity is O(N).

Problems

Problem: Roxor SRM 216 Level Three https://community.topcoder.com/stat?c=problem_statement&pm=2987&rd=5862 Editorial: https://www.topcoder.com/tc?module=Static&d1=match_editorials&d2=srm216

map<int,int> memo;
int n;

class Roxor { 
   public:
   int transform( int state, int i, int j, int k ) {
      state ^= (1 << i);
      state ^= (1 << j);
      state ^= (1 << k);
      return state;
   }
   int ifbit( int state, int i ) {
      return (state >> i)&1;
   }
   int winning( int state ) { // memoized search
      if( memo.count( state ) ) return memo[state];
      for( int i = 0; i < n-1; ++i ) {
         if( !ifbit( state, i ) ) continue;
         for( int j = i+1; j < n; ++j ) 
            for( int k = j; k < n; ++k ) 
               if( !winning( transform( state, i, j, k ) ) ) 
                  return memo[state] = 1;
      }
      return memo[state] = 0;
   }
   vector <int> play(vector <int> piles) // piles with stones
   {
      n = piles.size(); // <=15 given
      int state = 0; // state as a 15-bit integer
      for( int i = n-1; i >= 0; --i ) 
         state = state * 2 + piles[i]%2;
      memo.clear();
      for( int i = 0; i < n-1; ++i ) {
         if( !piles[i] ) continue;
         for( int j = i+1; j < n; ++j ) {
            for( int k = j; k < n; ++k ) {
               if( !winning( transform( state, i, j, k ) ) ) {
                  vector<int> ret( 3 );
                  ret[0] = i; ret[1] = j; ret[2] = k;
                  return ret;
               }
            }
         }
      }
      return vector<int>();
   } 
};

Reduction to Nim game

https://www.codechef.com/START51A/problems/CCGAME

Chef and Cook play a game on an array AA, alternating turns with Chef starting first. In one move, the player may choose indices 1 ≤ i < j ≤ N, subtract 1 from A_i, and add 1 to A_j. The player who cannot make a move loses.

Who wins with optimal play?

Solution

A couple of observations allow us to reduce the given game to a standard game of nim, whose solution is well-known.

Reduction For simplicity, let us say that we have N piles of stones, the i-th pile initially having A_i stones.

This gives us the desired reduction to nim: for each 1 ≤ i ≤ N, we have A_i piles of N−i stones, and then we simply find the solution to this nim game.

The above reduction to nim creates A_1 + A_2 + … +A_N piles in total, which is too large to store in memory.

However, since checking who wins a game of nim depends only on the bitwise XOR-sum of all the piles’ sizes, and we have the property x ⊕ x = 0 for any x, we can do the following: If A_i is even, it contributes an even number of N-i to the overall XOR-sum.

This makes the overall contribution of this position 0. If A_i is odd, it contributes an odd number of N−i to the overall XOR-sum.

The overall contribution of this position is thus just N−i. This gives us the final solution: compute the XOR of N−i across all i such that A_i is odd; let this value be X. Player 1 wins if X is non-zero, and Player 2 wins otherwise.

Tweedledum-Tweedledee Strategy

In some games, it is good idea to correspond every opponent’s move A with your move A, one-to-one, always perform the moves that mimics opponent’s, and win. This is the so-called Tweedledum-Tweedledee Strategy.

Ref: https://atcoder.jp/contests/abc278/editorial/5243

Young diagram

E - Candy Piles

source: https://atcoder.jp/contests/agc002/tasks/agc002_e

TODO:

Problems from https://letuskode.blogspot.com/2014/08/grundy-numbers.html

Dynamic subtraction: https://www.cs.cmu.edu/afs/cs/academic/class/15859-f01/www/notes/comb.pdf

https://sigma425.hatenablog.com/entry/2014/12/07/132702

https://blog.hamayanhamayan.com/entry/2017/02/27/025050

Check: https://web.mit.edu/sp.268/www/nim.pdf

REF: