Notes
DFS Tree
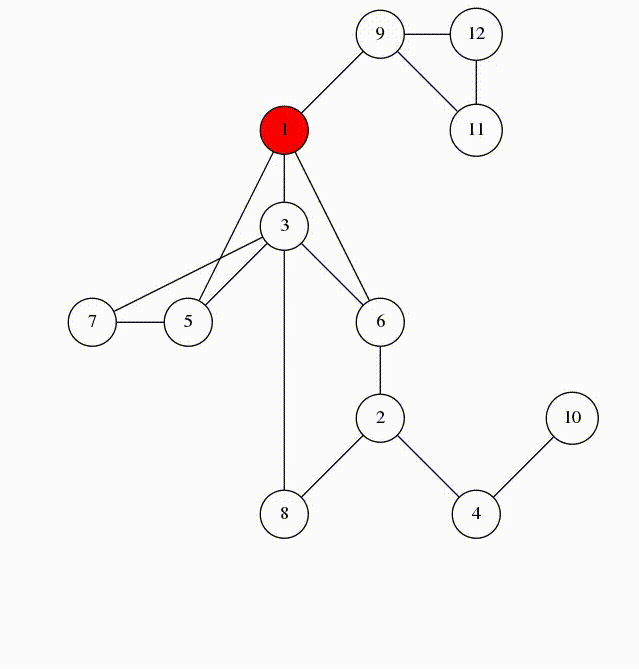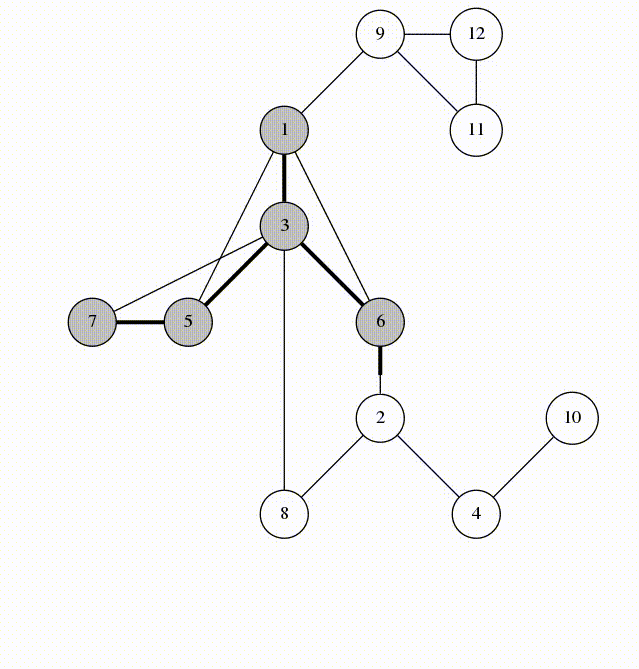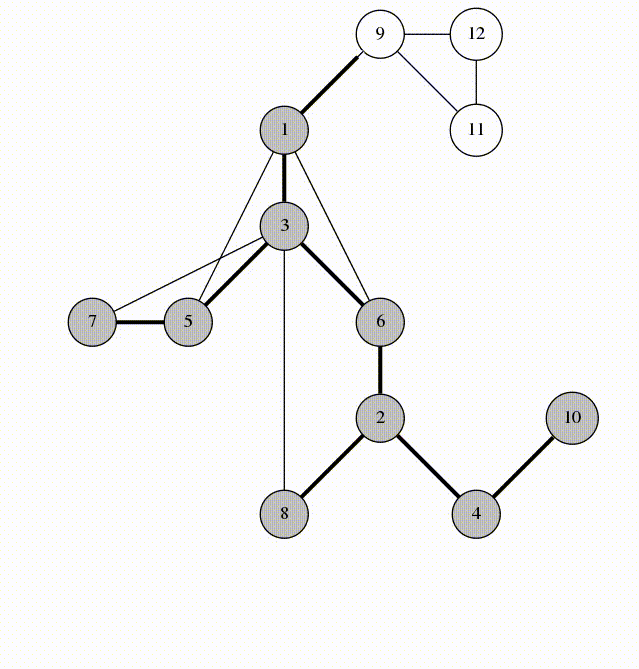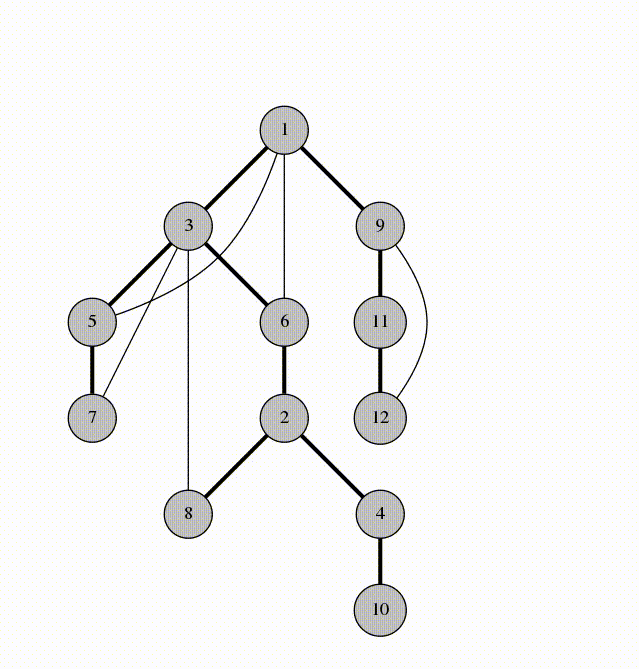

source: https://codeforces.com/blog/entry/68138

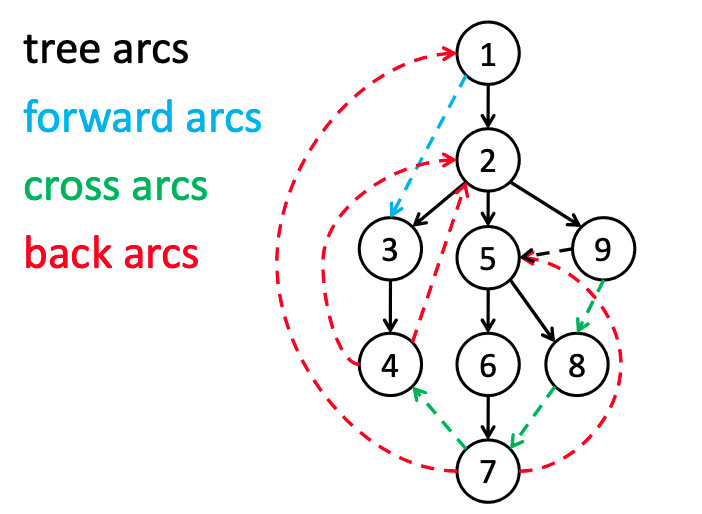
- In a depth-first search of an undirected graph G, every edge of G is either a tree edge or a back edge. Cross edges, Forward edges doesn't exist in un-directed graphs. Ref: CLRS
- Graph G has a cycle ⇔ DFS has a back edge
Finding cycle in (directed) graph
Use colors, for example, white, grey and black. You can even find the edges in the cycle. All the grey edges correspond to the cycle.
vector<vector<int>> Adj;
vector<int> V; // To store color of vertices (visited)
bool flag=true;
void dfs(int u){
V[u]=1; // GREY
for(int v:Adj[u]){
if(V[v]==1){ flag=false; // Cycle detected
// you found a cycle, it's easy to recover it now.
}
else if(V[v]==0) dfs(v);
}
V[u]=2; // BLACK
}
for(int i = 0; i < n; i++)
if(color[i] == 0) dfs(i, -1); // IF NODE IS WHITE, START NEW DFS
CSES Round Trip II
https://cses.fi/problemset/task/1678/const int nax = 1e5 + 10;
vector<int> adj[nax];
int col[nax];
vector<int> V;
void dfs(int u, int p){
col[u] = 1;
V.push_back(u);
for(int v:adj[u]){
if(col[v] == 0){
dfs(v, u);
} else if(col[v] == 1){
vector<int> cycle;
cycle.push_back(v);
while(V.back() != v){
cycle.push_back(V.back());
V.pop_back();
}
cycle.push_back(v);
printf("%d\n", cycle.size());
reverse(cycle.begin(), cycle.end());
for(int i:cycle) printf("%d ", i);
printf("\n");
exit(0);
}
}
col[u] = 2;
V.pop_back();
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
for(int i=0;i<m;i++){
int a, b; scanf("%d %d", &a, &b);
adj[a].push_back(b);
}
for(int i=1;i<=n;i++){
if(col[i] == 0) dfs(i, 0);
}
printf("IMPOSSIBLE\n");
return 0;
}
Implementation trick
- If you want to store vector of edges then you can store them as vector<pair<int,int>> V, {u,v}, then it is better to store them in {min(u,v), max(u,v)}.
Minimum number of nodes to reach all nodes
Given a Graph G(V, E). Find the smallest set of vertices from which all nodes in the graph are reachable.
-
Undirected graph: From each connected component we can consider one vertex. The minimum number of vertices will be equal to number of connected components in the graph.
-
Directed Acyclic graph: All vertices with
in_degree = 0constitute the set. All nodes with no in-degree must be in the final result, because they can not be reached from any other vertex. All the other nodes can be reached from some other nodes. All nodes which have an in-degree greater than 0 are reachable from a node that has an in-degree of 0.
Proof: Take any node 𝑋 that does not have an in-degree of 0. Take a node 𝑌 that has an edge connecting it to 𝑋. This node must exist as 𝑋 has a positive in-degree. Now all nodes that can reach 𝑌 can also reach 𝑋. Thus, we just need to prove that 𝑌 is reachable from a node with in-degree 0 to prove that 𝑋 is reachable from a node with in-degree 0. Repeat this process on the node 𝑌, taking it as the new 𝑋. Continue to do this until 𝑋 has an in-degree of 0. This process must end and find such an 𝑋 because there are only a finite number of nodes in the graph, and any repeated node within this process would indicate that there is a cycle in the graph. However as the graph is acyclic, this can not happen. Once we have found this 𝑋, we can say that 𝑋 is reachable from a node with an in-degree of 0 as it itself is a node within in-degree 0. We can then follow the graph to prove that the first 𝑋 is reachable from a node with in-degree 0. -
Directed graph: Considering vertices with indegree 0 may not be possible because of strongly connected components. For example in the following graph, no vertex has indegree zero. But if we start with any green vertex we can reach all the vertices.
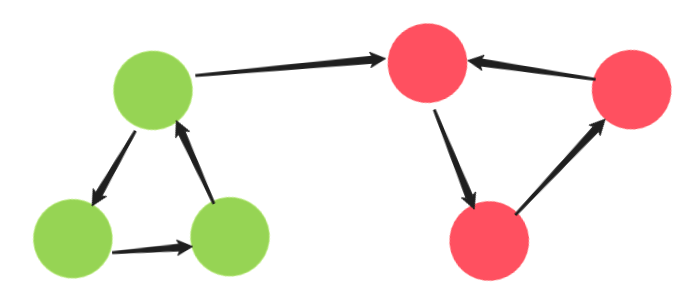
To solve this, we can compress all strongly connected components in the graph (using Tarjan's Algorithm or Kosaraju's Algorithm), leaving us with a directed acyclic graph. From this graph, it is enough if we consider vertices with
in_degree = 0.
DFS solution of DAG without using in_degree
class Solution:
def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
def dfs(g, c, vis, res):
vis[c] = True
for adj in g[c]:
if not vis[adj]:
dfs(g,adj,vis,res)
# adj can be visited by current vertex so we dont have to add adj in res
# only works in case of DAG
elif adj in res:res.remove(adj)
# Make a adjecency list from edge list
g = collections.defaultdict(list)
for e in edges:
u, v = e
g[u].append(v)
res = set() # smallest set of vertices
vis = [False]*n
for i in range(n):
if not vis[i]:
dfs(g, i, vis, res)
# add vertex from which we start traversing
res.add(i)
return list(res)
Anyways, This approach doesn't work for directed graphs because of SCC and cycles.
Def
Let G = (V; E) be a connected, undirected graph. An articulation point of G is a vertex whose removal disconnects G. A bridge of G is an edge whose removal disconnects G. A biconnected component of G is a maximal set of edges such that any two edges in the set lie on a common simple cycle, We can determine articulation points, bridges, and biconnected components using DFS.
Articulation Points/Cut Vertices and Bridges
An ‘Articulation Point’ is defined as a vertex in a graph G whose removal (all edges incident to this vertex are also removed) disconnects G. A graph without any articulation point is called ‘Biconnected’. Similarly, a ‘Bridge’ is defined as an edge in a graph G whose removal disconnects G. These two problems are usually defined for undirected graphs.
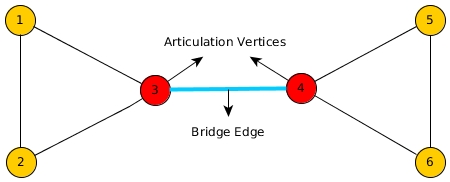
A simple approach to find bridges/articulation points would be to remove each point and check whether the graph is disconnected but it would take O(E(V+E)) time.
Observations:
A back-edge is never a bridge because a back-edge in an undirected graph is part of a cycle.
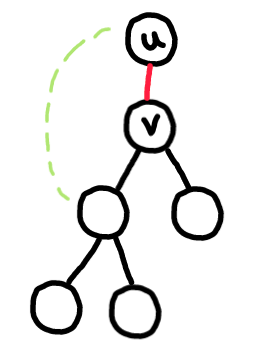
For edge (u, v) to be a bridge edge, there shouldn't be any back edge from subtree of v to u or above.
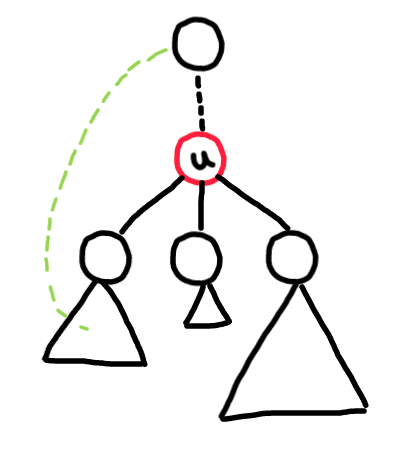
For vertex u to be an articulation vertex, there shouldn't be any backedge edge from subtree of some child of u to ancestors of u.
Implementation details:
We maintain two numbers dfs_num(u) and dfs_low(u). Here, dfs_num(u) stores the iteration counter when the vertex u is
visited for the first time, dfs_low(u) stores the lowest dfs_num rechable from the current DFS spanning subtree of u.
At the beginning, dfs_low(u) = dfs_num(u) when vertex u is visited for the first time. Then, dfs_low(u) can only be made
smaller if there is cycle(a back edge exists). Note that we do not update dfs_low(u) with a back edge (u, v) if v is a direct parent of u.
-
When we are in a vertex u with v as its neighbor and
dfs_low(v) ≥ dfs_num(u), thenuis an articulation vertex. This is because the fact thatdfs_low(v)is not smaller thandfs_num(u)implies that there is no back edge from vertexvthat can reach another vertexwwith a lowerdfs_num(w)thandfs_num(u). -
A vertex w with lower
dfs_num(w)than vertex u withdfs_num(u)implies thatwis the ancestor of u in the DFS spanning tree. This means that to reach the ancestor(s) ofufromv, one must pass through vertexu. Therefore, removing vertexuwill disconnect the graph.
However, there is one special case: The root of the DFS spanning tree (the vertex chosen as the start of DFS call) is an articulation point only if it has more than one children in the DFS spanning tree (a trivial case that is not detected by this algorithm).
vi dfs_num, dfs_low; // additional information for articulation points/bridges/SCCs
vi articulation_vertex, dfs_parent;
int dfsNumberCounter, dfsRoot, rootChildren;
void articulationPointAndBridge(int u) {
dfs_low[u] = dfs_num[u] = dfsNumberCounter++; // dfs_low[u] <= dfs_num[u]
for (int j = 0; j < (int) AdjList[u].size(); j++) {
ii v = AdjList[u][j];
if (dfs_num[v.first] == DFS_WHITE) { // a tree edge
dfs_parent[v.first] = u;
if (u == dfsRoot) rootChildren++; // special case, count children of root
articulationPointAndBridge(v.first);
if (dfs_low[v.first] >= dfs_num[u]) // for articulation point
articulation_vertex[u] = true; // store this information first
if (dfs_low[v.first] > dfs_num[u]) // for bridge
printf(" Edge (%d, %d) is a bridge\n", u, v.first);
dfs_low[u] = min(dfs_low[u], dfs_low[v.first]); // update dfs_low[u]
} else if (v.first != dfs_parent[u]) // a back edge and not direct cycle
dfs_low[u] = min(dfs_low[u], dfs_num[v.first]); // update dfs_low[u]
}
}
// inside main
dfsNumberCounter = 0;
dfs_num.assign(V, DFS_WHITE);
dfs_low.assign(V, 0);
dfs_parent.assign(V, -1);
articulation_vertex.assign(V, 0);
printf("Bridges:\n");
for (int i = 0; i < V; i++)
if (dfs_num[i] == DFS_WHITE) {
dfsRoot = i;
rootChildren = 0;
articulationPointAndBridge(i);
articulation_vertex[dfsRoot] = (rootChildren > 1);
} // special case
printf("Articulation Points:\n");
for (int i = 0; i < V; i++)
if (articulation_vertex[i])
printf(" Vertex %d\n", i);
The process to find bridges is similar. When dfs_low(v) > dfs_num(u), then edge u-v is
a bridge (notice that we remove the equality test ‘=’ for finding bridges).
source: https://github.com/remidinishanth/cp3files/blob/master/ch4/ch4/ch4_01_dfs.cpp
A demo of Tarjan's algorithm to find cut vertices. D denotes depth and L denotes lowpoint. Wiki
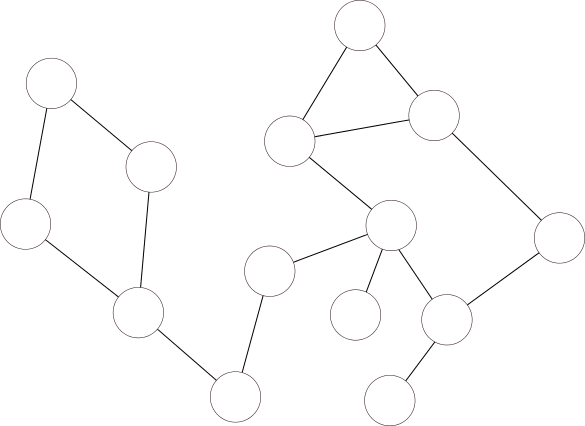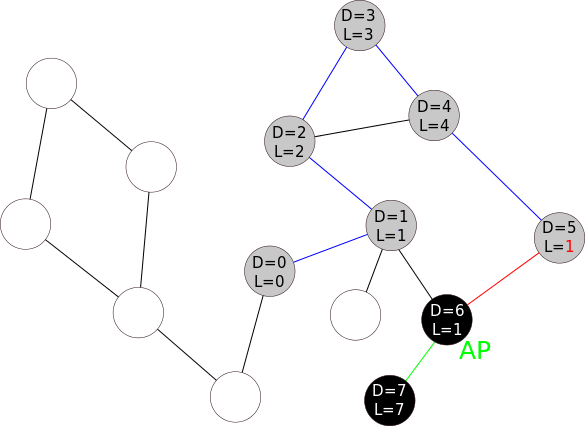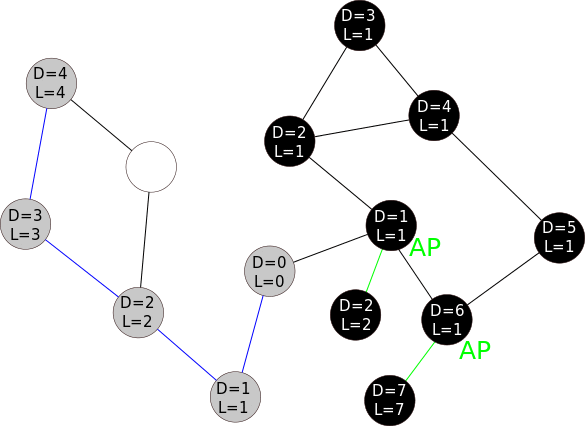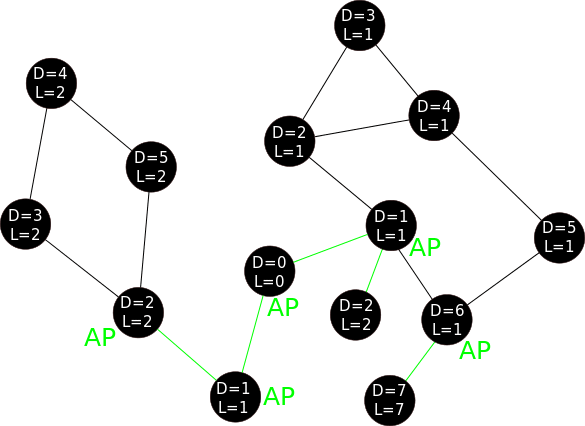
CP algorithms finding bridges
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
visited[to] = false- the edge is part of DFS tree;visited[to] = true && to ≠ parent- the edge is back edge to one of the ancestors;to = parent- the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] > tin[v])
IS_BRIDGE(v, to);
}
}
}
void find_bridges() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs(i);
}
}
Main function is find_bridges; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function IS_BRIDGE(a, b) is some function that will process the fact that edge (a,b) is a bridge, for example, print it.
Note that this implementation malfunctions if the graph has multiple edges, since it ignores them. Of course, multiple edges will never be a part of the answer, so IS_BRIDGE can check additionally that the reported bridge is not a multiple edge. Alternatively it's possible to pass to dfs the index of the edge used to enter the vertex instead of the parent vertex (and store the indices of all vertices).
CP algorithms finding articulation points
The implementation needs to distinguish three cases: when we go down the edge in DFS tree, when we find a back edge to an ancestor of the vertex and when we return to a parent of the vertex. These are the cases:
visited[to] = false- the edge is part of DFS tree;visited[to] = true && to ≠ parent- the edge is back edge to one of the ancestors;to = parent- the edge leads back to parent in DFS tree.
To implement this, we need a depth first search function which accepts the parent vertex of the current node.
int n; // number of nodes
vector<vector<int>> adj; // adjacency list of graph
vector<bool> visited;
vector<int> tin, low;
int timer;
void dfs(int v, int p = -1) {
visited[v] = true;
tin[v] = low[v] = timer++;
int children=0;
for (int to : adj[v]) {
if (to == p) continue;
if (visited[to]) {
low[v] = min(low[v], tin[to]);
} else {
dfs(to, v);
low[v] = min(low[v], low[to]);
if (low[to] >= tin[v] && p!=-1)
IS_CUTPOINT(v);
++children;
}
}
if(p == -1 && children > 1)
IS_CUTPOINT(v);
}
void find_cutpoints() {
timer = 0;
visited.assign(n, false);
tin.assign(n, -1);
low.assign(n, -1);
for (int i = 0; i < n; ++i) {
if (!visited[i])
dfs (i);
}
}
Main function is find_cutpoints; it performs necessary initialization and starts depth first search in each connected component of the graph.
Function IS_CUTPOINT(a) is some function that will process the fact that vertex a is an articulation point, for example, print it (Caution that this can be called multiple times for a vertex).
Another way of finding bridges is to count number of backedges going up from a vertex. Let's define dp[𝑢] as the number of back-edges passing over the edge between u and its parent. Then
dp[𝑢] = (# of back-edges going up from 𝑢) − (# of back-edges going down from 𝑢) + ∑(𝑣 is a child of 𝑢) dp[𝑣]
- (# of back-edges going up from 𝑢) is the number of back edges starting from u and going upwards
- (# of back-edges going down from 𝑢) is the number of backedges starting from some descendant of
uand reaching u.
The edge between 𝑢 and its parent is a bridge if and only if dp[𝑢] = 0.
Implementation
#include <iostream>
#include <vector>
using namespace std;
const int MAX_N = 100005;
vector < int > adj[MAX_N];
int lvl[MAX_N];
int dp[MAX_N];
bool bridge;
vector < pair < int, int >> ans;
void dfs(int vertex, int parent) {
lvl[vertex] = lvl[parent] + 1;
for (int nxt: adj[vertex]) {
if (lvl[nxt] != 0) {
if (nxt != parent) {
if (lvl[nxt] > lvl[vertex]) { // edge going downwards
dp[vertex]--;
ans.push_back(make_pair(nxt, vertex));
} else if (lvl[nxt] < lvl[vertex]) { // edge going upwards
dp[vertex]++;
}
}
} else { // tree edge
dfs(nxt, vertex);
ans.push_back(make_pair(vertex, nxt));
dp[vertex] += dp[nxt];
}
}
if (dp[vertex] == 0 && vertex != parent) {
bridge = true;
}
}
int main() {
int vertexc, edgec;
cin >> vertexc >> edgec;
for (int i = 0; i < edgec; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 1);
if (bridge) {
cout << 0 << endl;
} else {
for (pair < int, int > pr: ans) {
cout << pr.first << " " << pr.second << '\n';
}
}
}
source: https://codeforces.com/contest/118/submission/60187669, https://pastebin.com/ATwq4mJa
Applications
CF #89 Div 2E Bertown roads
You are given an undirected connected graph 𝐺. Direct all of its edges so that the resulting digraph is strongly connected, or declare that this is impossible. source: https://codeforces.com/contest/118/problem/E
Solution:
- If we have a bridge in the graph, then we can't orient the edges because say (u, v) is a bridge if we direct from u → v then there is no path from v to u.
- If there is no bridge in the graph, then the we can orient the edges. Let's form DFS tree starting from arbitrary vertex, we can direct all the tree edges downwards and back-edges upwards. This works because
- There is path from root to each vertex. By moving from root via tree edges
- There is a path from every vertex to the root, because there are no bridges there must be back edge going from vertex to its decendant, and from descendant we will have another backedge going up. We can just follow these backedges and get to the root.
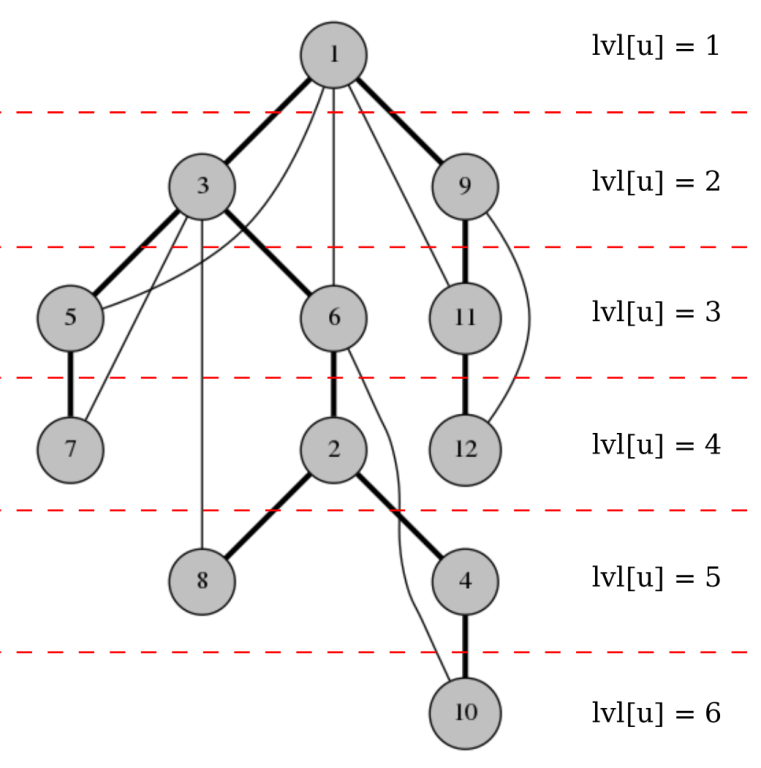
vector<vector<int>> Adj;
vector<bool> visited;
vector<int> depth;
vector<int> low;
vector<pair<int,int>> E;
bool ans = true; // true => there is no bridge
void dfs(int u, int p){
visited[u] = 1;
low[u] = depth[u] = depth[p] + 1;
for(int v:Adj[u]){
if(v == p) continue; // skip parent edge
if(visited[v]){ // back edge
if(depth[v] > depth[u])
E.push_back({v, u}); // orient upwards
low[u] = min(low[u], depth[v]);
}
else{
E.push_back({u, v}); // tree edge, orient downwards
dfs(v, u);
low[u] = min(low[u], low[v]); // update low value
if(low[v] > depth[u]){ // bridge exists
ans = false;
}
}
}
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
Adj = vector<vector<int>>(n+1, vector<int>());
visited = vector<bool>(n+1);
depth = vector<int>(n+1);
low = vector<int>(n+1);
for(int i=0;i<m;i++){
int u, v;
scanf("%d%d", &u, &v);
Adj[u].push_back(v);
Adj[v].push_back(u);
}
dfs(1, 0);
if(ans == false) return !printf("0\n");
for(auto [u, v]: E) printf("%d %d\n", u, v);
return 0;
}
CF #143 Div 2E Cactus
A cactus is a graph where every edge (or sometimes, vertex) belongs to at most one simple cycle. The first case is called an edge cactus, the second case is a vertex cactus. Cacti have a simpler structure than general graphs, as such it is easier to solve problems on them than on general graphs. But only on paper: cacti and cactus algorithms can be very annoying to implement if you don't think about what you are doing.
In the DFS tree of a cactus, for any span-edge, at most one back-edge passes over it. This puts cycles to an one-to-one correspondence with simple cycles:
- each back-edge forms a simple cycle together with the span-edges it passes over;
- there are no other simple cycles.
Problem: You are given a connected vertex cactus with 𝑁 vertices. Answer queries of the form "how many distinct simple paths exist from vertex 𝑝 to vertex 𝑞?".
Solution:
- If you learn the structure of these graphs, it is not hard to see, that if we’ll squeeze each cycle in one vertex, we get a tree. Let's mark the vertices in a cyle as black.
- Let's root the tree and for each vertex
u, calculate the number of black vertices on the path from the root tou; denote thiscnt[𝑢]. - the answer to query (𝑝,𝑞) is either
2^(cnt[𝑝]+cnt[𝑞]−2cnt[lca(𝑝,𝑞)])or2^(cnt[𝑝]+cnt[𝑞]−2cnt[lca(𝑝,𝑞)]+1)depending on the color of lca(𝑝,𝑞). Both of the cases can be combined to2^(cnt[𝑝]+cnt[𝑞]−cnt[lca(𝑝,𝑞)]-cnt[par[lca(𝑝,𝑞)]])
It's not hard to see why this approach works, the hard part is implementation
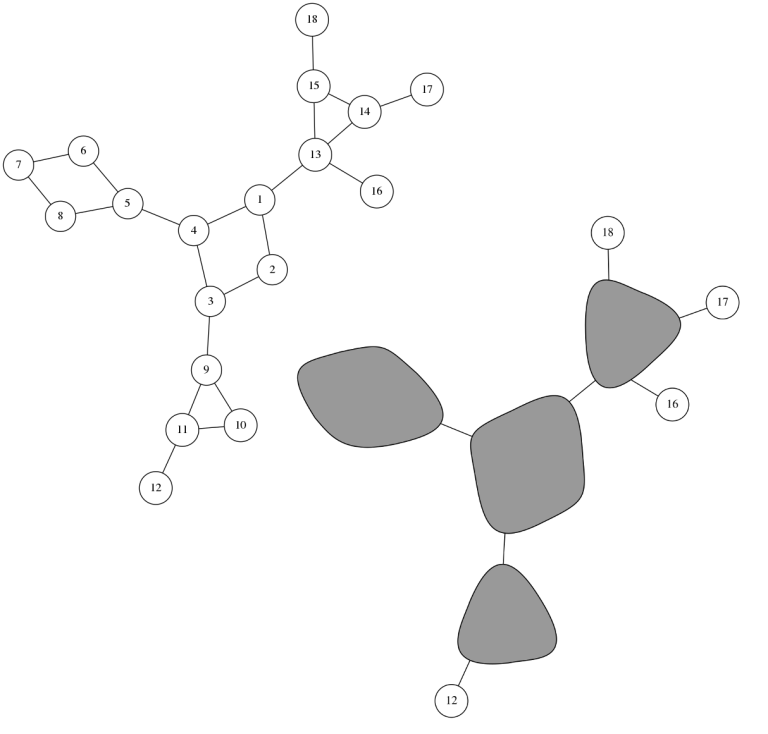
Since the given graph is vertex cactus, there can be atmost one back-edge going up from each vertex, because each edge/vertex is part of only one cycle. So we can do the following:
- give each back-edge an unique index starting from 𝑁+1;
- for each vertex 𝑢, calculate the index of the back-edge 𝑢 is under; call that cycleId[𝑢]; if 𝑢 isn't in a cycle then cycleId[𝑢]=𝑢;
- form a new adjacency list where for each 𝑢, each instance of 𝑢 is replaced by cycleId[𝑢].
def visit(u):
for v in children[u]:
visit(v)
if there is a back-edge going up from u:
cycleId[u] = the index of that back-edge
else:
cycleId[u] = u
for each vertex v among the children of u:
if cycleId[v] != v and there is no back-edge going down from v:
cycleId[u] = cycleId[v]
We can solve this problem by constructing bridge tree.
const int nax = 1e5 + 10;
vector<vector<int>> Adj;
int U[nax], V[nax]; // i-th edge is from U[i] to V[i]
int low[nax], depth[nax];
int bridge[nax];
int cnt[nax]; // number of elements in this bridge component
int comp[nax]; // bridge component id
int group = 1;
bool color[nax]; // 1 denotes black
int black[nax]; // number of black nodes from root
vector<vector<int>> Bdj; // bridge tree
const int LG = 20;
int par[nax][LG];
int adj(int e, int u){ // find other end of this edge
return U[e] ^ V[e] ^ u;
}
void find_bridges(int u, int p){
low[u] = depth[u] = depth[p] + 1;
for(int e: Adj[u]){
int v = adj(e, u);
if(v == p) continue;
if(depth[v] == 0){ // tree edge
find_bridges(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > depth[u]){
bridge[e] = true;
}
}else{ // back edge
low[u] = min(low[u], depth[v]);
}
}
}
void find_bridge_components(int u){
cnt[comp[u] = group]++;
for(int e:Adj[u]){
if(bridge[e]) continue;
int v = adj(e, u);
if(comp[v] == 0){
find_bridge_components(v);
}
}
}
void bridge_tree_dfs(int u, int p){
depth[u] = depth[p] + 1;
black[u] = black[p] + color[u];
for(int v:Bdj[u]){
if(v == p) continue;
par[v][0] = u;
for(int i=0; par[v][i]; i++){
int vpar = par[v][i];
par[v][i+1] = par[vpar][i];
}
bridge_tree_dfs(v, u);
}
}
int jump(int u, int d){
for(int i=LG-1; i>=0; i--){
if(d >= (1 << i)){
u = par[u][i];
d -= (1 << i);
}
}
return u;
}
int lca(int u, int v){
if(depth[u] > depth[v]) swap(u, v);
v = jump(v, depth[v] - depth[u]);
if(u == v) return u;
for(int i=LG-1; i>=0; i--){
if(par[u][i] != par[v][i]){
u = par[u][i];
v = par[v][i];
}
}
return par[u][0];
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
Adj = vector<vector<int>>(n+1, vector<int>());
for(int i=1; i<=m; i++){
int u, v;
scanf("%d %d", &u, &v);
U[i] = u; V[i] = v;
Adj[u].push_back(i);
Adj[v].push_back(i);
}
// Construct bridge tree
find_bridges(1, 0);
for(int i=1; i<=n; i++){
if(comp[i] == 0){
find_bridge_components(i);
color[group] = cnt[group] - 1;
group++;
}
}
Bdj = vector<vector<int>>(group+1, vector<int>());
for(int e=1; e<=m; e++){
if(bridge[e]){
int u = U[e], v = V[e];
int a = comp[u], b = comp[v];
Bdj[a].push_back(b);
Bdj[b].push_back(a);
}
}
bridge_tree_dfs(1, 0);
int md = 1e9 + 7;
vector<int> pow2(group+2, 1);
for(int i=1; i<group+2; i++){
pow2[i] = (pow2[i-1] * 2) % md;
}
int q;
scanf("%d", &q);
while(q--){
int u, v;
scanf("%d %d", &u, &v);
u = comp[u];
v = comp[v];
int l = lca(u, v);
int t = black[u] + black[v] - 2*black[l] + color[l];
printf("%d\n", pow2[t]);
}
return 0;
}
Bridge tree can also be computed by using stack variant of SCC algorithm https://codeforces.com/contest/231/submission/2329113
Cactus Not Enough
source: 2020-2021 ICPC, NERC, Northern Eurasia Onsite https://codeforces.com/contest/1510/problem/C
We are given a cactus(un-directed connected graph in which any two simple cycles have at most one vertex in common). Let's call a cactus strong if it is impossible to add an edge to it in such a way that it still remains a cactus. We want to find minimal number of edges that we can add to the given cactus to make it strong i. e. to create a new cactus with the same vertices, so that the original cactus is a subgraph of the new one, and it is impossible to add another edge to it so that the graph remains a cactus.
Solution: Let's look at some examples, Red edges indicate minimal edges that can be added.

Key observations:
- A strong cactus will only have cycles and paths of length 1. Consider all 2-vertex-connected components of the graph. If a graph is a cactus, each of them is either a cycle or a single edge. If there are two single-edge components that share a vertex, the graph isn’t a strong cactus, because an edge between these vertices can be added. On the other hand, if there are no such components, no edge could be added, because a path between the ends would cover at least one edge, which already lies on cycle, and this edge would lie on two cycles if we add the first edge. A more convenient form of the same statement is “a cactus is strong, iff after removing all edges lying on cycles, each connected component has at most one edge.”
- We can solve the problem for the tree formed by Biconnected components - split by cycles into tree subcomponents.
- We can ignore length 1 endpoints connecting to odd degree vertices. If the parent of a odd degree vertex is also odd, then other edges can be present in a cycle and hence this edge can be ignored.
We can find the cycles on the fly by storing low_value lowest depth vertex that can be reached while doing DFS similar to articulation points.
vector<vector<int>> Adj;
vector<int> depth, deg;
vector<pair<int,int>> paths;
pair<int,int> dfs(int u, int par){
if(par == -1) depth[u] = 0;
int cur_path = -1;
int low_val = depth[u];
for(int v:Adj[u]){
if(v == par) continue;
if(depth[v] == -1){
depth[v] = depth[u] + 1;
auto [ch_low_val, ch_path] = dfs(v, u);
low_val = min(low_val, ch_low_val);
if(ch_path != -1){
if(cur_path != -1){
paths.push_back({ch_path, cur_path});
cur_path = -1;
}else{
cur_path = ch_path;
}
}
}else if(depth[v] < depth[u]){ // update low_val
low_val = min(low_val, depth[v]);
}
}
if(low_val == depth[u] && par != -1){
if(deg[u] && deg[par]){
// both are odd degree, edge (par, u) can be ignored
deg[u]--; deg[par]--;
}else if(cur_path == -1){
cur_path = u;
}
}else{
if(cur_path != -1){
paths.push_back({cur_path, u});
cur_path = -1;
}
}
return {low_val, cur_path};
}
int main() {
while(true){
int n, m;
scanf("%d %d", &n, &m);
Adj = vector<vector<int>>(n+1, vector<int>());
depth = vector<int>(n+1, -1);
deg = vector<int>(n+1);
paths.clear();
if(n==0) break;
for(int i=0;i<m;i++){
int len, prev=-1;
scanf("%d", &len);
while(len--){
int x;
scanf("%d", &x);
if(prev!=-1){
Adj[x].push_back(prev);
Adj[prev].push_back(x);
}
prev = x;
}
}
for(int i=1;i<=n;i++) deg[i] = Adj[i].size() & 1;
dfs(1, -1);
printf("%d\n", (int)paths.size());
for(pair<int,int> x:paths){
printf("%d %d\n", x.first, x.second);
}
}
}
Bi-connectivity
Edge Biconnectivity: If any for pair of vertices (u, v) there exists two edge disjoint paths between u and v then graph is called edge biconnected. They can have common vertices in between but there should be atleast two edge disjoint paths between every (u, v).
- Given a un-weighted graph(directed or undirected), To find whether two vertices are edge biconnected, we can consider
uto be a source vertexvto be sink vertex and find max-flow betweenuandv, if the maximum flow iskthen there are exactlykedge disjoint paths betweenuandv.
Vertex Biconnectivity: For vertex biconnected graphs, there exists atleast two vertex disjoint paths between u and v.
- Given a un-weighted graph(directed or undirected), To find whether
uandvare vetex biconnected, we can break every vertexaintoaanda'and connect them with an edge. All the incoming edges ofago toaand all outgoing edges will go out froma'. Now we can max-flow betweenu'andv. Edge biconnectivity in modified graph leads to vertex biconnectivity in original graph.
Bi-connected graph: Equivalent definitions of a biconnected graph G
- Graph G has no separation edges(bridges) and no separation vertices(articulation points)
- For any two vertices u and v of G, there are two disjoint simple paths between u and v (i.e., two simple paths between u and v that share no other vertices or edges)
- For any two vertices u and v of G, there is a simple cycle containing u and v
Bi-connected components/ 2-connected components
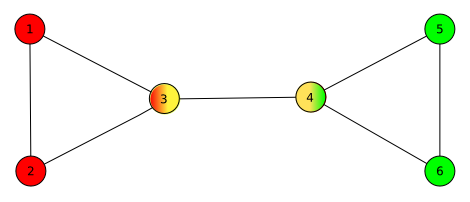
A biconnected component of a given graph is the maximal(as big as possible - not possible to make it larger) connected subgraph which doesn't contain any aritculation vertices, meaning that if any one vertex were to be removed, the graph will remain connected.
In the following diagram, different colours represent different biconnected components of the graph.
Interaction of biconnected components:
- An edge belongs to exactly one biconnected component
- A nonseparation vertex belongs to exactly one biconnected component
- A separation vertex belongs to two or more biconnected components
Any connected graph decomposes into a tree of biconnected components called the block-cut tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points.
Block Cut Tree: If each biconnected component of a given graph is shrinked into / represented as a single node called a block, and these blocks are attached to each other at shared vertices (articulation points), then the resulting tree formed is called a Block-Cut tree.
The following would be the block-cut tree of the above graph, where A,B,C are blocks attached to the articulation vertices 3 and 4.
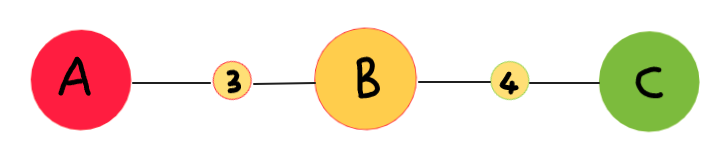
- A = represents vertices 1,2,3
- B = represents vertices 3,4
- C = represents vertices 4,5,6
REF: https://www.ics.uci.edu/~goodrich/teach/cs260P/notes/Biconnectivity.pdf
Bridge components
A bridge component of a given graph is the maximal connected subgraph which does not contain any bridge edges.
In the following graph, different coloured vertices lie in different bridge components. The black edges are the normal edges and blue edge represents the bridge edge separating different components.
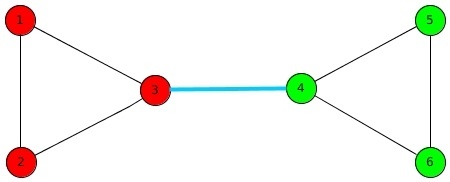
Bridge Tree: If each bridge component of a given graph is shrinked into/represented as a single node, and these nodes are connected to each other by the bridge edges which separated these components, then the resulting tree formed is called a Bridge Tree.
The following would be the bridge tree formed by shrinking the bridge components of the above given graph.

Can a bridge component have an articulation point?
Yes
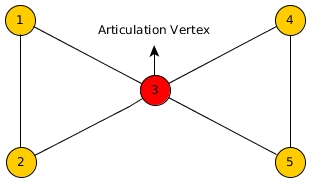
Properties of the Bridge Tree
- Each edge in the bridge tree is the one of the bridge edges in the original graph. Each edge in the normal graph G, is either a bridge tree edge or part of one of the bridge components.
- Since each node in the bridge tree is formed by shrinking the bridge components of original graph, therefore the bridge tree of a graph with N vertices can have at most N nodes (and N-1 edges).
- Bridge tree by construction is a tree, it cannot have cycles(No edge in a cylce cannot be a bridge).
- From the above point, it directly follows that a graph with N vertices can have at most N-1 bridges(because tree can have atmost N-1 edges).
- Within a bridge component, there is at least one way to orient all the edges such that there is a simple path from any node to any node within the component. (Non-trivial). Consider an arbitrary node and run a DFS, orient edges as you discover vertices. Because we don't have bridges within a bridge component , We have backedge from node to root of this DFS tree, We just orient tree edges going downward and backedges going upward and hence we can find the directed path.
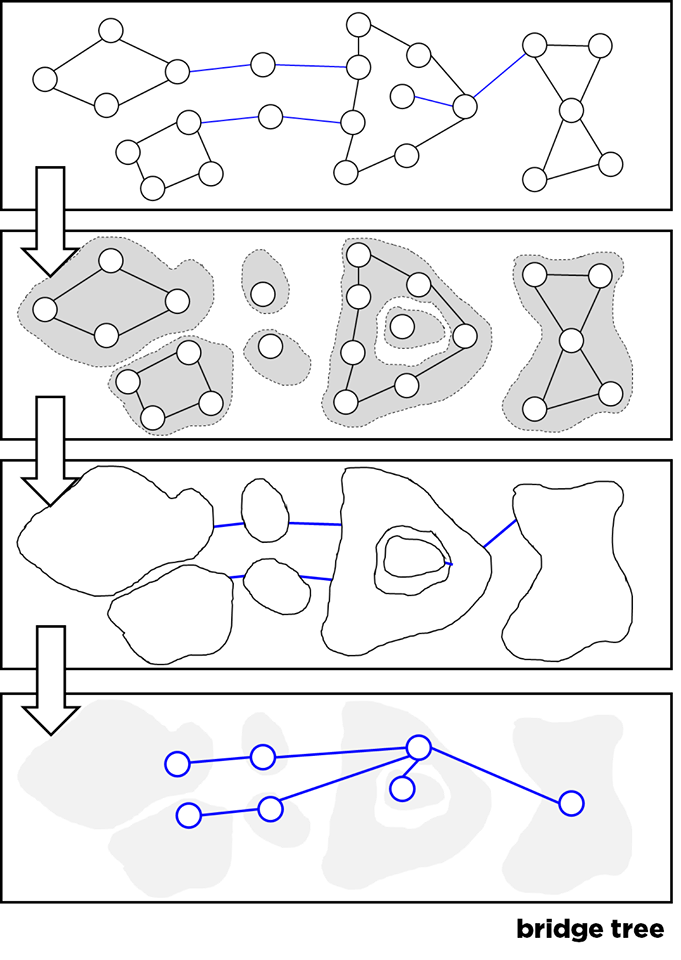
How to build bridge tree efficiently?
- Run bridge finding algorithm to find all the bridges. O(V + E)
- Remove all the bridges from G
- In the resulting graph, the nodes in two different bridge components now look disjoint. So just label all the nodes with their component id.
- Let the total number of these components be K
- Now add back the bridges into a new graph with these K nodes and you get B = (K, bridges) as your bridge tree
Runtime: O(V + E) or O((V + E)logE) if you use sets for Adjacency lists.
REF: https://tanujkhattar.wordpress.com/2016/01/10/the-bridge-tree-of-a-graph/, http://compalg.inf.elte.hu/~tony/Oktatas/TDK/FINAL/Chap%205.PDF, https://threadsiiithyderabad.quora.com/The-Bridge-Tree-of-a-graph
Tarjan's strongly connected components algorithm
Strong Connectivity applies only to directed graphs. A directed graph is strongly connected if there is a directed path from any vertex to every other vertex. There are at least two known algorithms to find SCCs: Kosaraju’s algorithm and Tarjan’s algorithm. In this section, we adopt Tarjan’s version, as it extends naturally from our previous discussion of finding Articulation Points and Bridges.
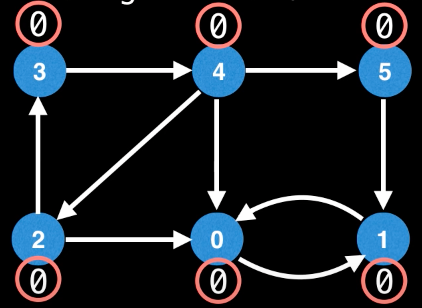
Consider the following graph, say we start DFS from the top-left vertex.
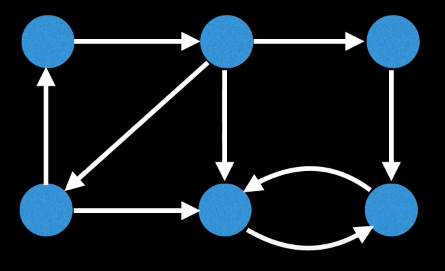
Assume that the vertices are visited in the following order.
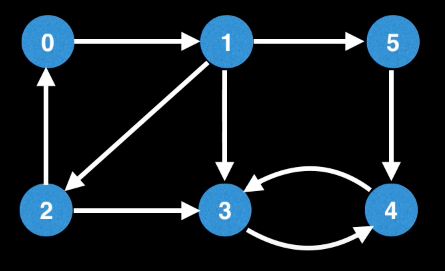
Let's find the low_link value(the smallest node_id reachable from that node) for each node.
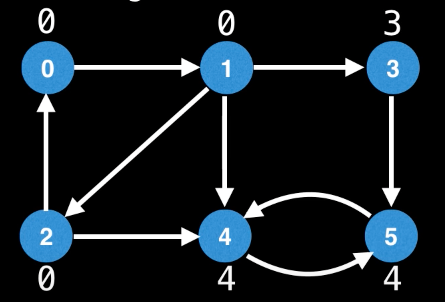
If we observe at the low_link value of the nodes, all the nodes in same SCC are having same low_link values.
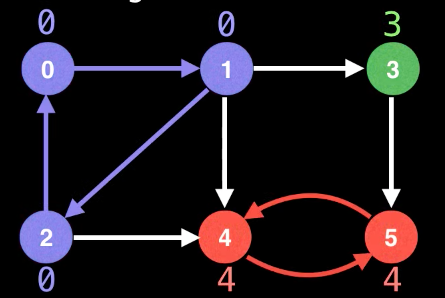
Can we use low_link values to find SCCs? There is a problem, low_link values depends on which vertex we start DFS, for example if the start with the bottom-middle node, then low_link values for all the nodes is same.
How to fix this? The Stack Invariant.
- To cope with the random traversal order of the DFS, Tarjan's algorithm maintains a set(often as a stack) of valid nodes from which to update low-link values from.
- Nodes are added to the set(stack) of valid nodes as they're explored for the first time.
- Nodes are removed from the set(stack) each time a complete SCC is found.
❗ New low-link update condition
- To update node u's
low_linkvalue to node v's value there has to be a path of edges fromutovand nodevmust be on the stack.
⚠️ Stack Invariant:
- The crucial invariant property is that a node remains on the stack after it has been visited if and only if there exists a path in the input graph from it to some node which was pushed earlier on the stack.
- In other words, it means that in the DFS a node would be only removed from the stack after all its connected paths have been traversed. When the DFS will backtrack it would remove the nodes on a single path and return to the root in order to start a new path.
At the end of the call that visits v and its descendants, we know whether v itself has a path to any node earlier on the stack. If so, the call returns, leaving v on the stack to preserve the invariant. If not, then v must be the root of its strongly connected component, which consists of v together with any nodes later on the stack than v (such nodes all have paths back to v but not to any earlier node, because if they had paths to earlier nodes then v would also have paths to earlier nodes which is false). The connected component rooted at v is then popped from the stack and returned, again preserving the invariant.
Implementation Details:
- On top of computing
dfs_num(u)anddfs_low(u)for each vertex, we also append vertexuto the back of a stackS(here the stack is implemented with a vector) and keep track of the vertices that are currently explored viavi visited.visited[u]tells whetheruis on the stack. - The condition to update
dfs_low(u)is slightly different from the previous DFS algorithm for finding articulation points and bridges. Here, only vertices that currently have visited flag turned on (part of the current SCC) that can updatedfs_low(u).
vi S, visited; // additional global variables
int numSCC;
void tarjanSCC(int u) {
dfs_low[u] = dfs_num[u] = dfsNumberCounter++; // dfs_low[u] <= dfs_num[u]
S.push_back(u); // stores u in a vector based on order of visitation
visited[u] = 1;
for (int j = 0; j < (int)AdjList[u].size(); j++) {
ii v = AdjList[u][j];
if (dfs_num[v.first] == DFS_WHITE)
tarjanSCC(v.first);
if (visited[v.first]) // condition for update, check if v.first in on stack
dfs_low[u] = min(dfs_low[u], dfs_low[v.first]);
}
if (dfs_low[u] == dfs_num[u]) { // if this is a root (start) of an SCC
printf("SCC %d:", ++numSCC); // this part is done after recursion
while (true) {
int v = S.back(); S.pop_back(); visited[v] = 0;
printf(" %d", v);
if (u == v) break;
}
printf("\n");
} }
Another readable implementation: https://yuihuang.com/cses-1682/
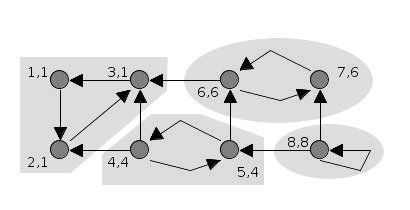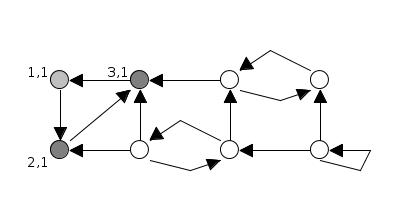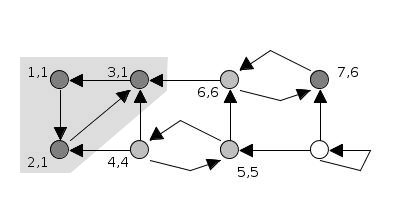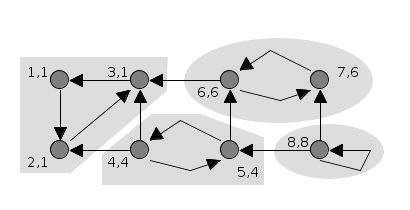
source: Wiki
Atcoder Library Implementation: https://atcoder.github.io/ac-library/document_en/scc.html and https://github.com/atcoder/ac-library/blob/master/atcoder/internal_scc.hpp
This returns "list of the vertices" sorted in topological order, i.e, for two vertices u, v in different strongly connected components, if there is a directed path from u to v, the list contains uu appears earlier than the list contains v.
Topological ordering might be useful in the following problem:
How many vertices can reach a strongly connected component with 2 or more vertices?
#include <bits/stdc++.h>
using namespace std;
int main(void) {
int n, m;
cin >> n >> m;
vector<vector<int> > e(n);
vector<int> out(n, 0);
int x, y, sz, cur;
for (int i = 0; i < m; i++) {
cin >> x >> y;
e[y - 1].push_back(x - 1);
out[x - 1]++;
}
queue<int>que;
int ans = n;
for (int i = 0; i < n; i++)if (out[i] == 0)que.push(i);
while (!que.empty()) {
ans--;
cur = que.front();
que.pop();
sz = e[cur].size();
for (int i = 0; i < sz; i++) {
out[e[cur][i]]--;
if (out[e[cur][i]] == 0)que.push(e[cur][i]);
}
}
cout << ans << endl;
return 0;
}
Check the solutions below for other/better implementations.
Problems
https://codeforces.com/contest/1534/problem/F1
My solution using map for storing index
int n, m;
map<int,vector<int>> Adj;
map<int,int> dfs_low, dfs_in;
int timer;
map<int, vector<int>> scc_comp;
const int nax = 5e5 + 10;
int comp_no[nax];
bool on_stack[nax];
vector<int> st; // stack
void dfs(int u){
dfs_low[u] = dfs_in[u] = timer++;
st.push_back(u);
on_stack[u] = true;
for(int v:Adj[u]){
if(dfs_in.find(v) == dfs_in.end()){
dfs(v);
dfs_low[u] = min(dfs_low[u], dfs_low[v]);
}
else if(on_stack[v]){
dfs_low[u] = min(dfs_low[u], dfs_low[v]);
}
}
if(dfs_low[u] == dfs_in[u]){ // SCC
while(true){
int x = st.back(); st.pop_back();
on_stack[x] = false;
scc_comp[u].push_back(x);
comp_no[x] = u;
if(x == u) break;
}
}
}
int f(int i, int j){
return m*i + j;
}
void add(int i1, int j1, int i2, int j2){
Adj[f(i1, j1)].push_back(f(i2, j2));
}
int main() {
sd2(n,m);
vector<string> V(n);
REP(i,n) cin >> V[i];
// ignore input
vi temp(m);
REP(i,m) sd(temp[i]);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(V[i][j] != '#') continue;
Adj[f(i,j)];
// up edge
if(i-1>=0 && V[i-1][j]=='#')
add(i, j, i-1, j);
// side edges
if(j-1 >= 0 && V[i][j-1]=='#') add(i, j, i, j-1);
if(j+1 < m && V[i][j+1]=='#') add(i, j, i, j+1);
// down edge
for(int k=1;i+k<n;k++){
if(j-1 >=0 && V[i+k][j-1]=='#') add(i, j, i+k, j-1);
if(j+1 < m && V[i+k][j+1]=='#') add(i, j, i+k, j+1);
if(V[i+k][j] == '#'){
add(i, j, i+k, j);
break;
}
}
}
}
memset(comp_no,-1,sizeof(comp_no));
for(auto [u, G]: Adj){
if(comp_no[u] == -1) dfs(u);
}
map<int, int> in_degree;
for(auto [u, G]: Adj){
in_degree[comp_no[u]];
for(int v:G){
if(comp_no[u] != comp_no[v])
in_degree[comp_no[v]]++;
}
}
int ans = 0;
for(auto [x, deg]: in_degree) if(deg == 0) ans++;
printf("%d\n", ans);
return 0;
}
Authors faster solution using arrays
Just store in[i][j] = index++; instead of i*m + j; This way indices will start from 0 and are continuous, can store them in an array. zjust like normal graph.
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
using pii = pair<int,int>;
using pll = pair<ll,ll>;
template<typename T>
int sz(const T &a){return int(a.size());}
const int MN=4e5+1;
vector<vector<char>> arr;
vector<vector<int>> ind;
int am[MN];
vector<int> adj[MN];
int nodecnt=0;
int id[MN],low[MN];
bool inst[MN];
vector<int> st;
int et;
int in[MN];
vector<vector<int>> comps;
int indeg[MN];
void dfs(int loc){
id[loc]=low[loc]=et++;
inst[loc]=true,st.push_back(loc);
for(auto x:adj[loc]){
if(!id[x])dfs(x),low[loc]=min(low[loc],low[x]);
else if(inst[x])low[loc]=min(low[loc],id[x]);
}
if(id[loc]==low[loc]){
comps.push_back({});
while(1){
int cur=st.back();
st.pop_back();
in[cur]=sz(comps)-1;
inst[cur]=false;
comps.back().push_back(cur);
if(cur==loc)break;
}
}
}
int main(){
cin.tie(NULL);
ios_base::sync_with_stdio(false);
int n,m;
cin>>n>>m;
arr.resize(n+1,vector<char>(m+1));
ind.resize(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>arr[i][j];
for(int i=1;i<=m;i++)cin>>am[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(arr[i][j]=='#'){
ind[i][j]=++nodecnt;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(arr[i][j]=='#'){
if(i-1>=1&&arr[i-1][j]=='#')adj[ind[i][j]].push_back(ind[i-1][j]);
for(int k=i+1;k<=n;k++){
if(arr[k][j]=='#'){
adj[ind[i][j]].push_back(ind[k][j]);
break;
}
}
bool leftdone=false,rightdone=false;
for(int k=i;k<=n&&(!leftdone||!rightdone)&&(arr[k][j]!='#'||k==i);k++){
if(j-1>=1&&!leftdone&&arr[k][j-1]=='#'){
adj[ind[i][j]].push_back(ind[k][j-1]),leftdone=true;
}
if(j+1<=m&&!rightdone&&arr[k][j+1]=='#'){
adj[ind[i][j]].push_back(ind[k][j+1]),rightdone=true;
}
}
}
}
}
et=1;
comps.push_back({});
for(int i=1;i<=nodecnt;i++)if(!id[i])dfs(i);
for(int i=1;i<sz(comps);i++){
for(auto x:comps[i])for(auto y:adj[x])if(in[y]!=i)indeg[in[y]]++;
}
int ans=0;
for(int i=1;i<sz(comps);i++){
if(indeg[i]==0)ans++;
}
printf("%d\n",ans);
return 0;
}
Kosaraju's Algorithm for SCC
Say we are given the following directed graph
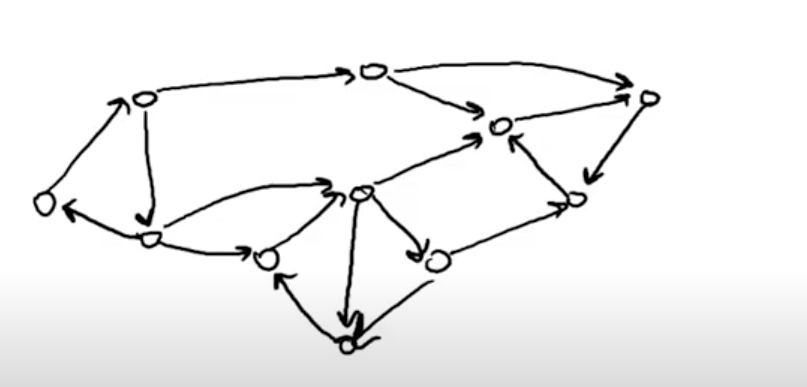
Say we start DFS from the red node, we visit all the nodes present in strongly connected component of this node.
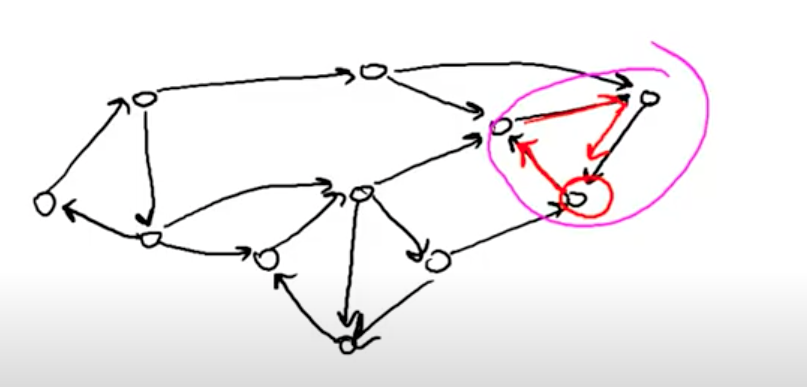
Say we start another DFS from the green node, we visit all the nodes present in the strongly connected of this node.
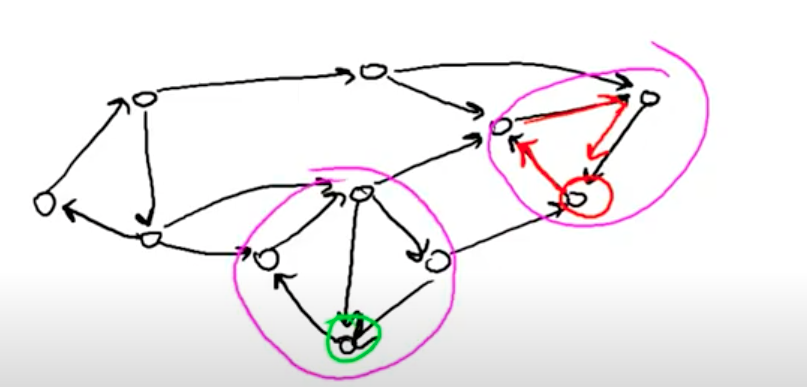
But we also have the blue edges, so we visit not only this strongly connected component but more than this. We might visit more than one strongly connected component.
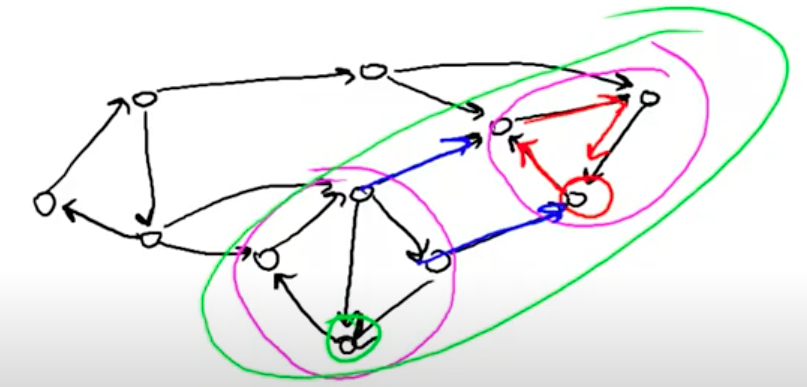
So we need a way to fix this ❓, we want to start the DFS at vertices such that we only visit vertices of this strongly connected component but not others. The idea is to use two DFS on the graph. First one is to find the order of the vertices. And do second DFS in this order of vertices we got from first DFS.
The first DFS is done on the original directed graph and record the ‘post-order’ traversal of the vertices as in finding topological sort. The second DFS is done on the transpose of the original directed graph using the ‘post-order’ ordering found by the first DFS. This two passes of DFS is enough to find the SCCs of the directed graph.
- Perform a DFS of G and number the vertices in order of completion of the recursive calls
- Construct a new directed graph rG by reversing the direction of every edge in G
- Perform a DFS on rG starting the search from the highest numbered vertex according to the decreasing order of finish time
- return DFS trees;

First DFS -> [c, g, f, h, d, b, e, a]
Nodes are traversed in [c, g, f, f', g, h, h', g', c, d, d', c', b, e, a, a', e', b'], where x denotes when x is visited and x' denotes end of vertex x. Finished order of vertices are [f', h', g', d', c', a', e', b'].
So we start second DFS in the order of [b, e, a, c, d, g, h, f]. Second DFS on transposed graph -> [b, a, e, c, d, g, f, h]
void Kosaraju(int u, int pass) { // pass = 1 (original), 2 (transpose)
dfs_num[u] = 1;
vii neighbor;
if (pass == 1) neighbor = AdjList[u]; else neighbor = AdjListT[u];
for (int j = 0; j < (int)neighbor.size(); j++) {
ii v = neighbor[j];
if (dfs_num[v.first] == DFS_WHITE)
Kosaraju(v.first, pass);
}
S.push_back(u); // as in finding topological order in Section 4.2.5
}
// inside main
AdjList.assign(N, vii());
AdjListT.assign(N, vii()); // the transposed graph
AdjList[V].push_back(ii(W, 1)); // always
AdjListT[W].push_back(ii(V, 1));
// run Kosaraju's SCC code here
S.clear(); // first pass is to record the `post-order' of original graph
dfs_num.assign(N, DFS_WHITE);
for (i = 0; i < N; i++)
if (dfs_num[i] == DFS_WHITE)
Kosaraju(i, 1);
numSCC = 0; // second pass: explore the SCCs based on first pass result
dfs_num.assign(N, DFS_WHITE);
for (i = N-1; i >= 0; i--)
if (dfs_num[S[i]] == DFS_WHITE) {
numSCC++;
Kosaraju(S[i], 2);
}
Brian bi t3nsor implementation
struct SCC {
int V, group_cnt;
vector<vector<int> > adj, radj;
vector<int> group_num, vis;
stack<int> stk;
// V = number of vertices
SCC(int V): V(V), group_cnt(0), group_num(V), vis(V), adj(V), radj(V) {}
// Call this to add an edge (0-based)
void add_edge(int v1, int v2) {
adj[v1].push_back(v2);
radj[v2].push_back(v1);
}
void fill_forward(int x) {
vis[x] = true;
for (int i = 0; i < adj[x].size(); i++) {
if (!vis[adj[x][i]]) {
fill_forward(adj[x][i]);
}
}
stk.push(x);
}
void fill_backward(int x) {
vis[x] = false;
group_num[x] = group_cnt;
for (int i = 0; i < radj[x].size(); i++) {
if (vis[radj[x][i]]) {
fill_backward(radj[x][i]);
}
}
}
// Returns number of strongly connected components.
// After this is called, group_num contains component assignments (0-based)
int get_scc() {
for (int i = 0; i < V; i++) {
if (!vis[i]) fill_forward(i);
}
group_cnt = 0;
while (!stk.empty()) {
if (vis[stk.top()]) {
fill_backward(stk.top());
group_cnt++;
}
stk.pop();
}
return group_cnt;
}
};
source: https://github.com/t3nsor/codebook/blob/master/scc.cpp
Constructing Condensed Graph
How to construct the condensed graph efficiently after finding SCC? https://codeforces.com/blog/entry/9566
We can obviously use a vector<set<int>> adj and the do adj[comp[u]].insert(comp[v]), Finally we can copy set into a vector. Can we do it without using set?
fill(mark, false)
for c in components:
for v in c:
for u in original_edges(v):
if non mark[comp(u)]:
# If edge is not added to comp(v)
add_comp_edge(c, comp(u))
mark[comp(u)] = true
# Reset all the marks for next iteration
for v in c:
for u in original_edges(v):
mark[comp(u)] = false
Applications
- How many vertices can reach a strongly connected component with 2 or more vertices?
The following approach doesn't built SCC.
Consider repeatedly performing the following operation of writing integers on vertices of graph G given in the input as many times as possible. Initially, no vertex has an integer written on it.
In the i-th operation, find “a vertex of G such that no integer is yet written on it, and it has no outgoing edges or every vertices pointed by its outgoing edges has an integer written on it.” If such a vertex exists, write i on it; if not, terminate the sequence of operations without performing the (i+1)-th operation.
The sequence of operations terminates after at most N operations.
When it is terminated, by the conditions of writing integers, every vertex with an integer written on it has no outgoing edges, or every destination of its outgoing edges has a smaller integer. Thus, no matter which edge he chooses, he will reach another vertex with a strictly smaller integer written on it. Therefore, from a vertex with i written on it, Takahashi can travel at most (i−1) times. Thus, he can only move finite number of times.
If you implement it naively, it will cost O(NM) time, which will not finish in the time limit. Here, note that once a vertex satisfied the condition for an integer to be written, the vertex never becomes invalid until an integer is actually written. So consider repeating putting the vertices that satisfied the condition to a queue, popping vertices as much as possible from the queue, and writing integers on them.
When implementing the solution above, it is easier to reverse the edges.
#include <bits/stdc++.h>
using namespace std;
int main(void) {
int n, m;
cin >> n >> m;
vector<vector<int> > e(n);
vector<int> out(n, 0);
int x, y, sz, cur;
for (int i = 0; i < m; i++) {
// edge goes from x to y
// we store the reverse edges
cin >> x >> y;
e[y - 1].push_back(x - 1);
out[x - 1]++;
}
queue<int> que;
int ans = n;
for (int i = 0; i < n; i++)
if (out[i] == 0)
que.push(i);
while (!que.empty()) {
ans--;
cur = que.front();
que.pop();
sz = e[cur].size();
for (int i = 0; i < sz; i++) {
out[e[cur][i]]--;
if (out[e[cur][i]] == 0)
que.push(e[cur][i]);
}
}
cout << ans << endl;
return 0;
}
Alternate easy explanation: Suppose that we have a vertex with indegree 0, then we can safely remove it, because it is not part of the answer, when we remove this vertex, some other vertices degree might become zero, continue this process.