Notes

Heavy-light decomposition

The heavy-light (H-L) decomposition of a rooted tree is a method of partitioning the vertices of the tree into disjoint paths (all vertices have degree two, except the endpoints of a path, with degree one) that gives important asymptotic time bounds for certain problems involving trees.

The heavy-light decomposition of a tree T=(V, E) is a coloring of the tree's edges. Each edge is either heavy or light.

Motivation

Problem 1: Suppose we are given a tree where each node is having some value, we want to answer queries like the sum of values on nodes on the path from u to v.

We can calculate LCA and find the answer by breaking path(u,v) into path(u, lca) and path(lca, v), now Calc(u,v) = Calc(u, root) + Calc(v, root) - 2 Calc(root, LCA(u,v)).

But say we also have an update query set(v,x) where we are given node v and value x, and we need to update the value of node v to x. Now we can't use LCA to answer efficiently.

Say instead of a tree, we just have a chain(set of nodes connected one after another), we can support both calc(u,v) and set(v,x) by using BIT/Segment tree.

Key: HLD supports updating the tree node/edge values unlike the LCA sparse array approach, but the tree structure is fixed.

Problem 2: Suppose we have a rooted tree with weights at each node. Answer a series of queries that either update the value at a node, or query the maximum value along a path from a node to the root.

The naive solution to this problem is to simply walk up that path from a node to the root and calculate the maximum value along the path. This solution has runs in O(1) time for updates and O(n) time for queries, which is too slow for multiple queries.

The problem of finding the maximum value along a path is a signal that segment trees might be useful, but how do we make a segment tree from a tree? We will do this using a technique called heavy light decomposition.

Basic idea

We will divide the tree into vertex-disjoint chains (meaning no two chains has a node in common) in such a way that to move from any node in the tree to the root node, we will have to change at most log N chains. To put it in other words, if the path from any node to root can be broken into pieces such that each piece belongs to only one chain, then we will have no more than log N pieces.

We already know that queries in each chain can be answered with O(log N) complexity and there are at most log N chains we need to consider per path. So on the whole we have O(log^2 N) complexity solution.

What does this decomposition accomplish?

Imagine that you are traveling down the tree, starting at the root. How many times can you use a light edge? Clearly, log N is an upper bound, because each time you use a light edge the number of vertices in your subtree is at least halved.

We will show that for any vertex v the path from v to the root only contains at most log N light edges. Now imagine that as we walk along the path from v to the root, we are keeping track of the important path we are on. This only changes when we use a light edge. And as there are at most log N light edges on our path, we only change the important path at most log N times.

Almost the same is true for a path between two arbitrary vertices v and w: Let x be their least common ancestor in the rooted tree. The path from v to w can be split into two paths, v to x and x to w. Each of these two paths only uses edges from at most log N important paths, hence the entire path from v to w crosses at most 2log N important paths.

For each heavy path, we will keep an interval tree, hence to answer a query, we first identify the segments of heavy paths it uses. This can be done in O(log N). Then we process each segment separately. Processing each segment involves two queries on the interval tree for its important path, hence the total time complexity is O(log^2 N) per query.

source: https://ipsc.ksp.sk/2009/real/solutions/l.html IPSC 2009 problem L in http://ipsc.ksp.sk/archive

We can solve problems involving queries on Trees

Two school of thoughts

There are two ways to label edges as heavy or light.

1. For each vertex that isn’t a leaf, find the edge that leads to the child with the largest subtree (breaking ties arbitrarily) and call it heavy.

2. Consider the edge's two endpoints: one is closer to the root, and one is further away. If the size of the subtree rooted at the latter is more than half that of the subtree rooted at the former, the edge is heavy. Otherwise, it is light.

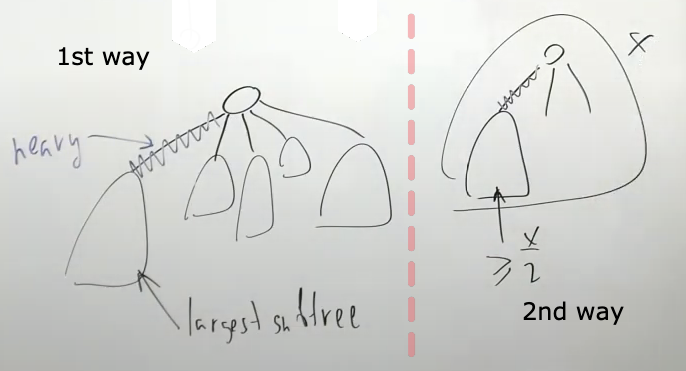
In the first case, we'll have many heavy edges and hence our code will run faster, in the second case we might have not any heavy edges for some trees.

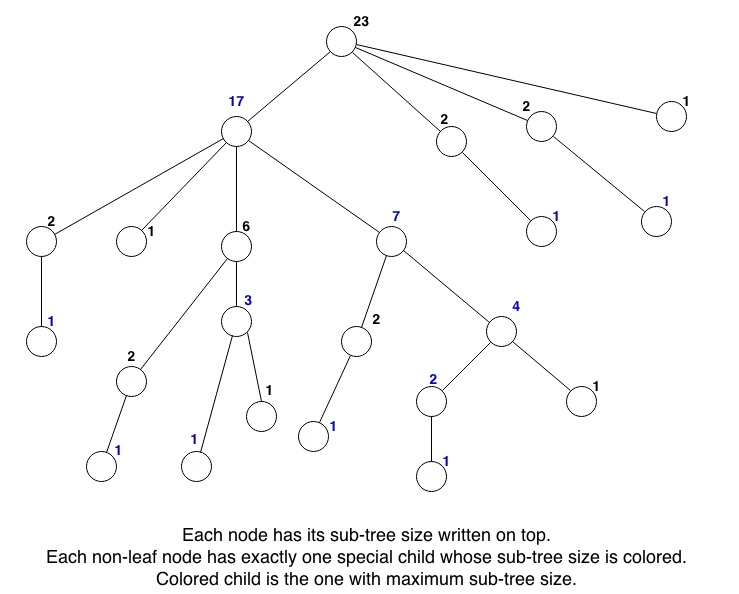
Based on the subtree sizes, mark the edges as heavy, breaking ties arbitrarily.

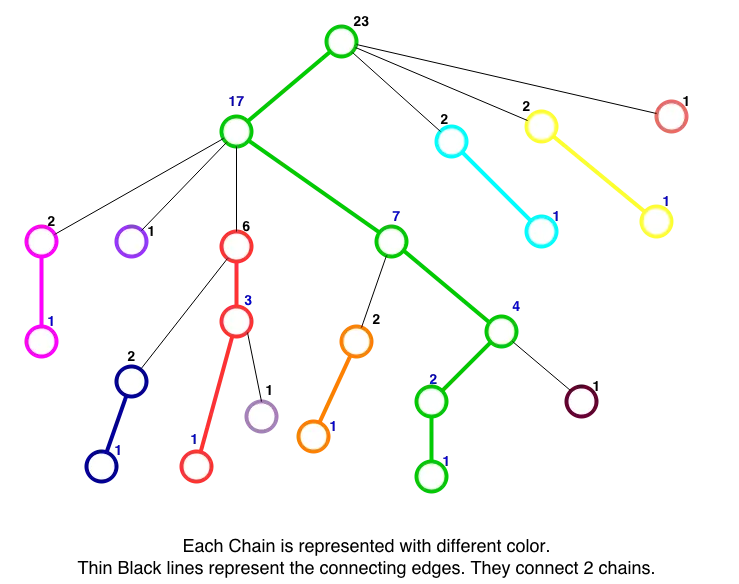
Consider some node, if you choose heavy edge and go down, we will have heavy paths. Using these, our tree nodes can be split into heavy paths, along with some single leaf nodes(these can be thought of as paths of size 1). Since every vertex has exactly one heavy edge, we can decompose the tree into disjoint paths consisting of heavy edges.

Now the key idea about this setup is that any path on the tree will pass through at most O(log n) light edges. By extension, each path also passes through at most O(log n) vertical chains. Note that since each light subtree has size n/2 and heavy paths are connected by light edges, any path from a node to the root of the tree will pass through at most log N heavy paths.

One useful idea for the proof of this claim is that you can break any path 𝑢 -> 𝑣 on a tree into two (possibly non-existent) components: the path from u up to 𝑙𝑐𝑎(𝑢,𝑣) and the path from v up to 𝑙𝑐𝑎(𝑢,𝑣), where 𝑙𝑐𝑎(𝑢,𝑣) is the lowest common ancestor of u and v. Because 𝑙𝑐𝑎(𝑢,𝑣) is an ancestor of both u and v, both of these separate paths will also be vertical chains themselves. So now let's prove that both of these vertical chains only pass through 𝑂(log n) light edges.

Proof

Consider some vertex v in some vertical chain. Let the size of its subtree be x and its parent be p. If the edge from v to p is light, then there must be some other child u of p with subtree size y, where y ≥ x. Then when we move up to p, the size of p's subtree is at least x+y ≥ 2x. So whenever we move up a light edge, the size of our current subtree is at least doubled. Because the size of a subtree can't be more than n, we end up moving up a light edge at most O(log n) times.

Psuedo code to calculate heavy edges

def go(x):
  sz = 1
  for y in children[x]:
    y_sz = go(y)
    sz += y_sz
    if y_sz > max:
      max = y_sz
      heavy[x] = y
  return sz

Psuedo code for segment trees on chains

Instead of using many small segments trees(one for each chain), we can just use one segment tree.

We first recursively build for the heavy node and then for all other subtrees.

def go2(x):
  p.append(x)
  if not children[x].empty():
    go2(heavy[x])
    for y in children[x]:
      if y != heavy[x]:
        go2(x)

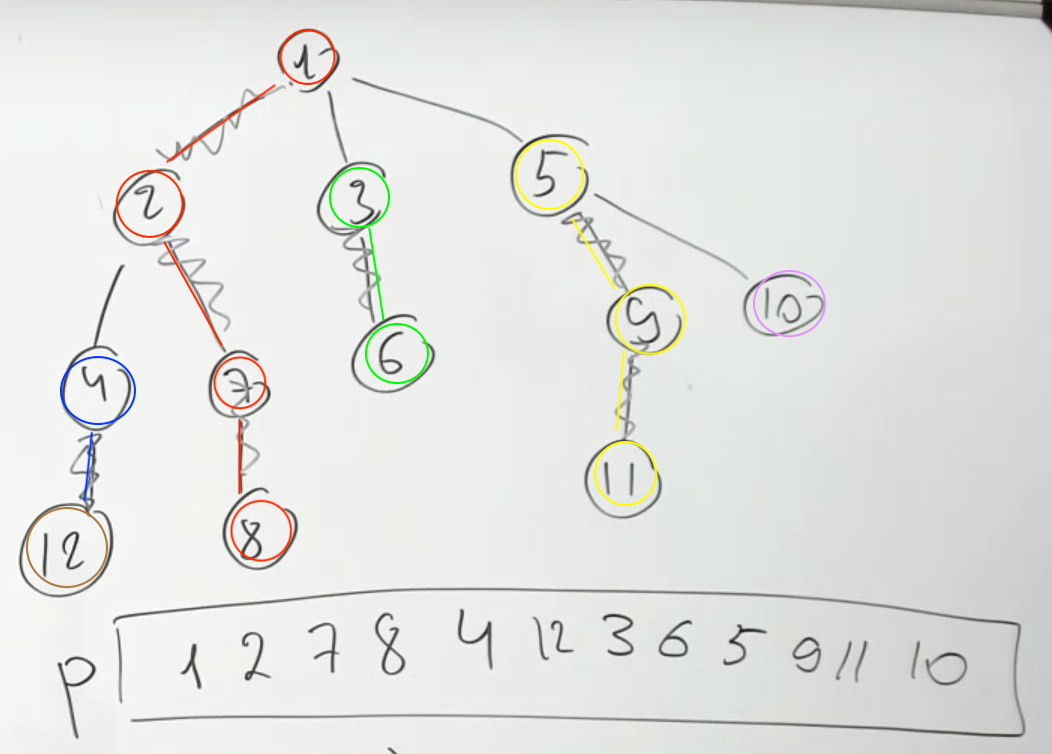
If you look at array p, it can be breaked into heavy chains segments. For two nodes within a chain, we can directly query segment tree to find the result. Also we can just use one segement tree for the whole graph instead of using one for each heavy chain.

It turns out that we don't need any special code to calculate LCA and answer the queries, we can leverage HLD to do it. From each node let's have a pointer to the top node in the heavy path. For node u let's call this top node of chain as top[u](We can find this in the same recursive procedure, see Adamant's trick).

If both u and v are on the same heavy chain, then we can query Segment tree and get the answer, otherwise, since they belong to different chains, we just move to the top[deeper_node] continue.

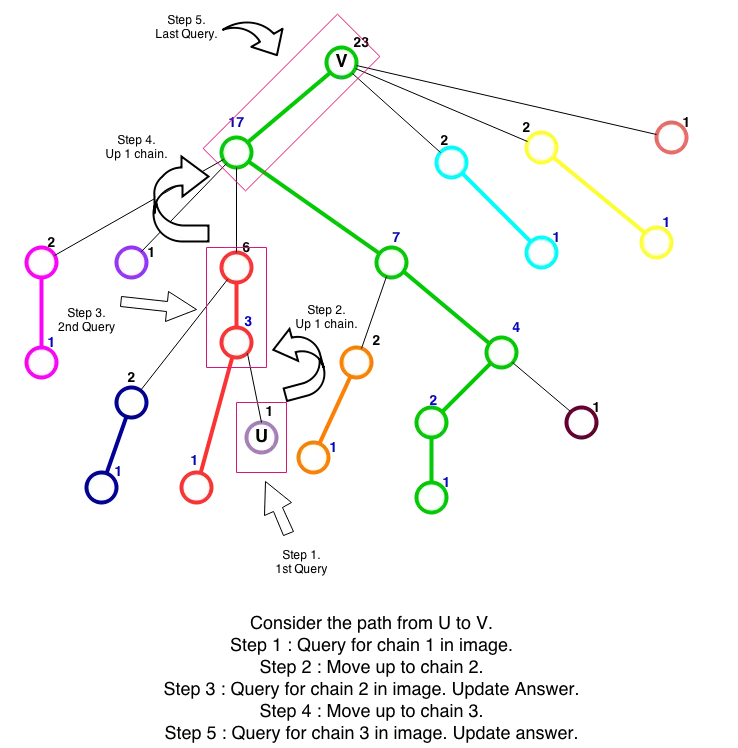
while True:
  x = top[u]
  y = top[v]
  if x == y:
    # u and v belong to same heavy chain
    res += sum(u,v) # sum is call to segment tree
    break
  if d[x] > d[y]: # d[x] is depth from the root
    res += sum(u,x)
    u = x.parent
  else:
    res += sum(y,v)
    v = y.parent

The above works because if depth[x] > depth[y] then lca(u,v) is at higher depth than x and hence we can safely add the values from u to x to the answer and move to node above x. The lca(u,v) can be computed from HLD of tree as follows:

int lca(int i, int j)
{
    while (chain[i] != chain[j])
        if (depth[head[i]] > depth[head[j]])
            i = parent[head[i]];
        else
            j = parent[head[j]];
 
    return depth[i] < depth[j] ? i : j;
}

The above python pseudo code can be further simplified to, here when querying segment tree in sum we'll need to use pos[v] instead of v

def process_path(u, v):
    while top[u] != top[v]:
        if depth[top[u]] > depth[top[v]]:
	    swap(u, v)
	res += sum(top[v], v)
    # u and v are now in same chain
    if depth[u] > depth[v]:
        swap(u, v)
    res += sum(u, v)

Here head[i] is the top[i], for more details refer complete code.

Complete code

#include <algorithm>
#include <numeric>
 
#include <iostream>
#include <sstream>
#include <string>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <stack>
 
#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cassert>
 
#include <cmath>
#include <complex>
using namespace std;
 
const int V = 100000;
vector<int> adj[V];     // adjacency list
int parent[V], heavy[V];
int depth[V], size[V];  
int chain[V], head[V];  
//Where chain[u] is u's chain number and head[u] is the node closest to root in u's chain.
 
void DFS(int i)
{
    size[i] = 1;
    for (int k=0; k<adj[i].size(); ++k)
    {
        int j = adj[i][k];
        if (j == parent[i]) continue;
 
        parent[j] = i;
        depth[j] = depth[i] + 1;
 
        DFS(j);
 
        size[i] += size[j];
        if (heavy[i] == -1 || size[j] > size[heavy[i]]) 
            heavy[i] = j;
    }
}
 
void heavylight_DFS(int N)
{
    memset(heavy, -1, sizeof(heavy));
 
    parent[0] = -1;
    depth[0] = 0;
    DFS(0);
 
    int c = 0;  
    for (int i=0; i<N; ++i)
        if (parent[i] == -1 || heavy[parent[i]] != i)
        {
            for (int k = i; k != -1; k = heavy[k])
                chain[k] = c, head[k] = i;
            c++;
        }
}
 
int q[V], *qf, *qb; // BFS queue
 
void heavylight_BFS(int N)
{
    qf = qb = q;
    parent[0] = -1;
    depth[0] = 0;
    *qb++ = 0;
    while (qf < qb)
        for (int i=*qf++, k=0; k<adj[i].size(); ++k)
        {
            int j = adj[i][k];
            if (j == parent[i]) continue;
            parent[j] = i;
            depth[j] = depth[i] + 1;
            *qb++ = j;
        }
 
    memset(size, 0, sizeof(size));
    memset(heavy, -1, sizeof(heavy));
    for (int k=N-1; k>0; --k)   
    {
        int j = q[k], i = parent[q[k]];
        size[j]++;
        size[i] += size[j];
        if (heavy[i] == -1 || size[j] > size[heavy[i]])
            heavy[i] = j;
    }
 
    int c = 0;
    for (int i=0; i<N; ++i)
        if (parent[i] == -1 || heavy[parent[i]] != i)
        {
            for (int k = i; k != -1; k = heavy[k])
                chain[k] = c, head[k] = i;
            c++;
        }
}
 
int lca_1(int i, int j)
{
    while (chain[i] != chain[j])
        if (depth[head[i]] > depth[head[j]])
            i = parent[head[i]];
        else
            j = parent[head[j]];
 
    return depth[i] < depth[j] ? i : j;
}
 
int lca_2(int i, int j)
{
    while (chain[i] != chain[j])
    {
        if (depth[head[i]] > depth[head[j]])
            swap(i, j);
        j = parent[head[j]];
    }
 
    if (depth[i] > depth[j])
        swap(i, j);
    return i;
}
 
void look_inside(int N) {
	int i;
 
	printf("\n");
	printf("HEAVY: \n");
	printf("(i, j): i----(heavy edge)----j\n\n");
 
	for (i = 0; i < N; i++)
		printf("(%d, %d)\n", i, heavy[i]);
	
	printf("\n");
	printf("CHAIN: \n");
	printf("(i, j): Node i is in group (heavy-path group) number j\n\n");
	
	for (i = 0; i < N; i++)
		printf("(%d, %d)\n", i, chain[i]);
 
	printf("\n");
	printf("HEAD: \n");
	printf("(i, j): Node i goes up all the way to the highest node (j) which is in the same group\n\n");
 
	for (i = 0; i < N; i++)
		printf("(%d, %d)\n", i, head[i]);
}
 
int main() {
	int N, i, j;
	FILE *fin = fopen("input.txt", "r");
 
	fscanf(fin, "%d", &N);
 
	for (i = 0; i < N; i++)
		adj[i].clear(); 
	while (fscanf(fin, "%d%d", &i, &j) != EOF) {
		adj[i].push_back(j);
		adj[j].push_back(i); 
	}
 
	//heavylight_DFS(N);
	heavylight_BFS(N);
 
	//printf("%d\n", lca_2(12, 16));
 
	//printf("%d\n", lca_2(16, 12));
 
	//printf("%d\n", lca_2(0, 7));
 
	//printf("%d\n", lca_2(0, 24));
 
	printf("%d\n", lca_1(6635, 8590));
 
	//look_inside(N); //I just added it into this program in order to understand more about how it works
}

source: https://apps.topcoder.com/forums/?module=Thread&threadID=796128&start=0&mc=8

AI cash CPP implementation

// root[v] = top[v] the node with lowest depth in the heavy chain containing v

template <class T, int V>
class HeavyLight {
  int parent[V], heavy[V], depth[V];
  int root[V], treePos[V];
  SegmentTree<T> tree;

  template <class G>
  int dfs(const G& graph, int v) {
    int size = 1, maxSubtree = 0;
    for (int u : graph[v]) if (u != parent[v]) {
      parent[u] = v;
      depth[u] = depth[v] + 1;
      int subtree = dfs(graph, u);
      if (subtree > maxSubtree) heavy[v] = u, maxSubtree = subtree;
      size += subtree;
    }
    return size;
  }

  template <class BinaryOperation>
  void processPath(int u, int v, BinaryOperation op) {
    for (; root[u] != root[v]; v = parent[root[v]]) {
      if (depth[root[u]] > depth[root[v]]) swap(u, v);
      op(treePos[root[v]], treePos[v] + 1);
    }
    // root[u] == root[v], same chain, query in Segtree
    if (depth[u] > depth[v]) swap(u, v); 
    op(treePos[u], treePos[v] + 1);
  }

public:
  template <class G>
  void init(const G& graph) {
    int n = graph.size();
    fill_n(heavy, n, -1);
    parent[0] = -1;
    depth[0] = 0;
    // find heavy chains
    dfs(graph, 0);
    // update top[v]
    for (int i = 0, currentPos = 0; i < n; ++i)
      if (parent[i] == -1 || heavy[parent[i]] != i)
        for (int j = i; j != -1; j = heavy[j]) {
          root[j] = i;
          treePos[j] = currentPos++;
        }
    tree.init(n);
  }

  void set(int v, const T& value) {
    tree.set(treePos[v], value);
  }

  void modifyPath(int u, int v, const T& value) {
    processPath(u, v, [this, &value](int l, int r) { tree.modify(l, r, value); });
  }

  T queryPath(int u, int v) {
    T res = T();
    processPath(u, v, [this, &res](int l, int r) { res.add(tree.query(l, r)); });
    return res;
  }
};

source: https://codeforces.com/blog/entry/22072 & https://codeforces.com/contest/484/submission/24715608

Extra care must be taken in processPath if the binary operation isn't commutative, you'll need two segment trees, one for downward sums and one for upward sums.

Remarks

Note that this only works if the tree is fixed. You have to make your decomposition in advance, then put all the range trees on it.

If you want to be able to modify the tree as well as one of your operations, you can use a more advanced data structure called a link-cut tree. The link-cut tree effectively maintains the special paths just as we have, but it does with splay trees, and in such a way that the paths can be spliced up and put back together in different ways. Amazingly, the link-cut tree actually achieves O(log n) time per query (no square in there!)

Applications

If you can solve the problem for a chain using a segment tree, then there is a very good chance that you can solve the problem for a tree using HLD

Dynamic distance query

Consider the following problem: A weighted, rooted tree is given followed by a large number of queries and modifications interspersed with each other. A query asks for the distance between a given pair of nodes and a modification changes the weight of a specified edge to a new (specified) value. How can the queries and modifications be performed efficiently?

First of all, we notice that the distance between nodes u and v is given by dist(u,v) = dist(root,u) + dist(root, v) - 2* dist(root, LCA(u,v)). There are a number of techniques for efficiently answering lowest common ancestor queries, so if we can efficiently solve queries of a node's distance from the root, a solution to this problem follows trivially.

To solve this simpler problem of querying the distance from the root to a given node, we augment our walk procedure as follows: when following a light edge, simply add its distance to a running total; when following a heavy path, add all the distances along the edges traversed to the running total (as well as the distance along the light edge at the top, if any). The latter can be performed efficiently, along with modifications, if each heavy path is augmented with a data structure such as a segment tree or binary indexed tree (in which the individual array elements correspond to the weights of the edges of the heavy path).

This gives O(log^2 n) time for queries. It consists of two "skips" and a LCA query. In the "skips", we may have to ascend logarithmically many heavy paths each of which takes logarithmic time, and so we need O(log^2 n) time. An update, merely an update to the underlying array structure, takes O(log n) time.

Adamant's implementation trick

This tries to combine the ideas from Euler tour tree, so that we can query subtrees while we query subpaths. Here nxt[v] is the top vertex in the heavy chain from v.

void dfs_sz(int v = 0) {
    sz[v] = 1;
    for(auto &u: g[v]) {
        dfs_sz(u);
        sz[v] += sz[u];
        if(sz[u] > sz[g[v][0]]) {
            swap(u, g[v][0]);
        }
    }
}

void dfs_hld(int v = 0) {
    in[v] = t++;
    for(auto u: g[v]) {
        nxt[u] = (u == g[v][0] ? nxt[v] : u);
        dfs_hld(u);
    }
    out[v] = t;
}

Then you will have array such that subtree of v correspond to segment [in_v; out_v) and the path from v to the last vertex in ascending heavy path from v (which is nxt_v) will be [in_nxt_v; in_v] subsegment which gives you the opportunity to process queries on pathes and subtrees simultaneously in the same segment tree.

With the above implementation we can solve the following problem: Given a tree on n vertices and q queries of form

1. add x to all numbers in the subtree
2. add x to all numbers on the path
3. find maximum number in the subtree
4. find maximum number on the path,

We can answer all queries in O((n + q) log^2n) because batch updates may be performed over subtrees and arbitrary paths across the tree simultaneously using the single segment tree built across the traversal of the tree.

source: https://codeforces.com/blog/entry/53170

Implementations

Benq's cpp implementation

// loops
#define FOR(i,a,b) for (int i = (a); i < (b); ++i)
#define F0R(i,a) FOR(i,0,a)
#define ROF(i,a,b) for (int i = (b)-1; i >= (a); --i)
#define R0F(i,a) ROF(i,0,a)
#define rep(a) F0R(_,a)
#define each(a,x) for (auto& a: x)

/**
 * Description: 1D range increment and sum query.
 * Source: USACO Counting Haybales
 * Verification: SPOJ Horrible
 */

template<class T, int SZ> struct LazySeg { 
	static_assert(pct(SZ) == 1); // SZ must be power of 2
	const T ID = 0; T comb(T a, T b) { return a+b; }
	T seg[2*SZ], lazy[2*SZ]; 
	LazySeg() { F0R(i,2*SZ) seg[i] = lazy[i] = ID; }
	void push(int ind, int L, int R) { /// modify values for current node
		seg[ind] += (R-L+1)*lazy[ind]; // dependent on operation
		if (L != R) F0R(i,2) lazy[2*ind+i] += lazy[ind]; /// prop to children
		lazy[ind] = 0; 
	} // recalc values for current node
	void pull(int ind) { seg[ind] = comb(seg[2*ind],seg[2*ind+1]); }
	void build() { ROF(i,1,SZ) pull(i); }
	void upd(int lo,int hi,T inc,int ind=1,int L=0, int R=SZ-1) {
		push(ind,L,R); if (hi < L || R < lo) return;
		if (lo <= L && R <= hi) { 
			lazy[ind] = inc; push(ind,L,R); return; }
		int M = (L+R)/2; upd(lo,hi,inc,2*ind,L,M); 
		upd(lo,hi,inc,2*ind+1,M+1,R); pull(ind);
	}
	T query(int lo, int hi, int ind=1, int L=0, int R=SZ-1) {
		push(ind,L,R); if (lo > R || L > hi) return ID;
		if (lo <= L && R <= hi) return seg[ind];
		int M = (L+R)/2; 
		return comb(query(lo,hi,2*ind,L,M),query(lo,hi,2*ind+1,M+1,R));
	}
};

/**
 * Description: Heavy-Light Decomposition, add val to verts 
 	* and query sum in path/subtree.
 * Time: any tree path is split into $O(\log N)$ parts
 * Source: http://codeforces.com/blog/entry/22072, https://codeforces.com/blog/entry/53170
 * Verification: *
 */

template<int SZ, bool VALS_IN_EDGES> struct HLD { 
	int N; vi adj[SZ];
	int par[SZ], root[SZ], depth[SZ], sz[SZ], ti;
	int pos[SZ]; vi rpos; // rpos not used, but could be useful
	void ae(int x, int y) { adj[x].pb(y), adj[y].pb(x); }
	void dfsSz(int x) { 
		sz[x] = 1; 
		each(y,adj[x]) {
			par[y] = x; depth[y] = depth[x]+1;
			adj[y].erase(find(all(adj[y]),x)); // remove parent from adj list
			dfsSz(y); sz[x] += sz[y];
			if (sz[y] > sz[adj[x][0]]) swap(y,adj[x][0]);
		}
	}
	void dfsHld(int x) {
		pos[x] = ti++; rpos.pb(x);
		each(y,adj[x]) {
			root[y] = (y == adj[x][0] ? root[x] : y);
			dfsHld(y); }
	}
	void init(int _N, int R = 0) { N = _N; 
		par[R] = depth[R] = ti = 0; dfsSz(R); 
		root[R] = R; dfsHld(R); 
	}
	int lca(int x, int y) {
		for (; root[x] != root[y]; y = par[root[y]])
			if (depth[root[x]] > depth[root[y]]) swap(x,y);
		return depth[x] < depth[y] ? x : y;
	}
	/// int dist(int x, int y) { // # edges on path
	/// 	return depth[x]+depth[y]-2*depth[lca(x,y)]; }
	LazySeg<ll,SZ> tree; // segtree for sum
	template <class BinaryOp>
	void processPath(int x, int y, BinaryOp op) {
		for (; root[x] != root[y]; y = par[root[y]]) {
			if (depth[root[x]] > depth[root[y]]) swap(x,y);
			op(pos[root[y]],pos[y]); }
		if (depth[x] > depth[y]) swap(x,y);
		op(pos[x]+VALS_IN_EDGES,pos[y]); 
	}
	void modifyPath(int x, int y, int v) { 
		processPath(x,y,[this,&v](int l, int r) { 
			tree.upd(l,r,v); }); }
	ll queryPath(int x, int y) { 
		ll res = 0; processPath(x,y,[this,&res](int l, int r) { 
			res += tree.query(l,r); });
		return res; }
	void modifySubtree(int x, int v) { 
		tree.upd(pos[x]+VALS_IN_EDGES,pos[x]+sz[x]-1,v); }
};

source: https://github.com/bqi343/USACO/blob/master/Implementations/content/graphs%20(12)/Trees%20(10)/HLD%20(10.3).h, https://usaco.guide/plat/hld?lang=cpp

Problem: 1553. Caves and Tunnels

Problem: https://acm.timus.ru/problem.aspx?space=1&num=1553

source: https://codeforces.com/blog/entry/12239, https://ideone.com/KgO3Kj

#pragma comment(linker,"/STACK:100000000000,100000000000")

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <cmath>
#include <map>
#include <stack>
#include <set>
#include <iomanip>
#include <queue>
#include <map>
#include <functional>
#include <list>
#include <sstream>
#include <ctime>
#include <climits>
#include <bitset>
#include <list>
#include <cassert>
#include <complex>

using namespace std;

/* Constants begin */
const long long inf = 1e18+7;
const long long mod = 1e9+7;
const double eps = 1e-9;
const double PI = 2*acos(0.0);
const double E = 2.71828;
/* Constants end */

/* Defines begin */
#define pb push_back
#define mp make_pair
#define ll long long
#define double long double
#define F first
#define S second
#define all(a) (a).begin(),(a).end()
#define forn(i,n) for (int (i)=0;(i)<(ll)(n);(i)++)
#define random (rand()<<16|rand())
#define sqr(x) (x)*(x)
#define base complex<double>
/* Defines end */

int n, m;
vector<int> g[100005];
int val[100005];
int nxt[100005], size[100005], p[100005], chain[100005], num[100005], csz[100005], top[100005], all, cnt = 1, depth[100005];
ll t[400005], mx[400005];

// segment tree update
void upd(int v, int tl, int tr, int pos, int d){
  if(tl == tr){
    t[v] += d;
    return;
  }
  int tm = (tl + tr) >> 1;
  if(pos <= tm) upd(v + v, tl, tm, pos, d); else
    upd(v + v + 1, tm + 1, tr, pos, d);
  t[v] = max(t[v + v], t[v + v + 1]);
}

// segment tree get
ll go(int v, int tl, int tr, int l, int r){
  if(l > tr || r < tl){
    return 0;
  }
  if(l <= tl && r >= tr){
    return t[v];
  }
  int tm = (tl + tr) >> 1;
  return max(go(v + v, tl, tm, l, r), go(v + v + 1, tm + 1, tr, l, r));
}

// dfs to computer heavy chains using size
void dfs(int v, int pr = 0){
  p[v] = pr;
  size[v] = 1;
  forn(i, g[v].size()){
    int to = g[v][i];
    if(to == pr){
      continue;
    }
    depth[to] = depth[v] + 1;
    dfs(to, v);
    size[v] += size[to];
    if(nxt[v] == -1 || size[to] > size[nxt[v]]){
      nxt[v] = to;
    }
  }
}

// dfs to compute decompostion
void hld(int v, int pr = -1){
  chain[v] = cnt - 1; // chain v belong to (cnt-1)th chain
  num[v] = all++; // position in segement tree
  if(!csz[cnt - 1]){
    top[cnt - 1] = v; // top of (cnt-1)th chain
  }
  ++csz[cnt - 1]; // size of (cnt-1)th chain
  if(nxt[v] != -1){
    hld(nxt[v], v);
  }
  forn(i, g[v].size()){
    int to = g[v][i];
    if(to == pr || to == nxt[v]){
      continue;
    }
    ++cnt;
    hld(to, v);
  }
}

// computing result on some path
ll go(int a, int b){
  ll res = 0;
  while(chain[a] != chain[b]){
    if(depth[top[chain[a]]] < depth[top[chain[b]]]) swap(a, b);
    int start = top[chain[a]];
    if(num[a] == num[start] + csz[chain[a]] - 1)
      res = max(res, mx[chain[a]]);
    else
      res = max(res, go(1, 0, n - 1, num[start], num[a]));
    a = p[start];
  }
  if(depth[a] > depth[b]) swap(a, b);
  res = max(res, go(1, 0, n - 1, num[a], num[b]));
  return res;
}

void modify(int a, int b){
  upd(1, 0, n - 1, num[a], b);
  int start = num[top[chain[a]]];
  int end = start + csz[chain[a]] - 1;
  mx[chain[a]] = go(1, 0, n - 1, start, end);
}

int main(void) {
  #ifdef nobik
    freopen("input.txt", "rt", stdin);
    freopen("output.txt", "wt", stdout);
  #endif
  scanf("%d", &n);
  forn(i, n - 1){
    int a, b; scanf("%d %d", &a, &b); --a; --b;
    g[a].pb(b); g[b].pb(a);
  }
  memset(nxt, -1, sizeof nxt);
  dfs(0);
  hld(0);
  scanf("%d", &m);
  forn(i, m){
    char c;
    scanf(" %c", &c);
    if(c == 'G'){
      int a, b; scanf("%d %d", &a, &b); --a; --b;
      printf("%lld\n", go(a, b));
    } else {
      int a, b; scanf("%d %d", &a, &b); --a;
      modify(a, b);
    }
  }
  return 0;
}

Edge List representation based

Thanuj Khattar Baba's code

int U[N], V[N], W[N], baseArray[N], DP[LOGN][N], level[N], sub[N];
int chainParent[N], chainHead[N], blen, chainNo[N], pos[N], nchain;
// U[i], V[i], W[i] -- represents a single edge i going from node U[i] to V[i]
// with weight W[i].
vector<int> g[N];
// g[U[i]].push_back(i);
// g[V[i]].push_back(i);
int adj(int x, int e) {
  // returns node adjacent to x on the edge e.
  return x ^ U[e] ^ V[e];
}
void HLD(int u, int ee) {  // edge list graph.graph is 1-based.
  baseArray[blen] = W[ee];
  pos[u] = blen;
  blen++;
  chainNo[u] = nchain;
  int sc = -1, mx = 0; // sc - special child/heavy child
  for (auto e : g[u]) {
    if (e == ee) continue; // parent
    int w = adj(u, e);
    if (sub[w] > mx) sc = e, mx = sub[w];
  }
  if (sc == -1) return; // leaf node
  HLD(adj(u, sc), sc);
  for (auto e : g[u]) {
    if (e == ee || e == sc) continue;
    int w = adj(u, e);
    nchain++;
    chainParent[nchain] = u; // chainParent is the node connecting the light edge
    chainHead[nchain] = w; // the top node of this chain
    HLD(w, e);
  }
}
void dfs(int u, int ee) {
  sub[u] = 1;
  for (auto e : g[u]) {
    if (e == ee) continue;
    int w = adj(u, e);
    level[w] = level[u] + 1;
    DP[0][w] = u;
    dfs(w, e);
    sub[u] += sub[w];
  }
}
void preprocess() {
  DP[0][1] = 1; // LCA table
  dfs(1, 0);
  chainHead[nchain] = chainParent[nchain] = 1;
  HLD(1, 0);
  // Build the LCA DP table here.
}

Also check out https://cp-algorithms.com/graph/hld.html for simple implementation

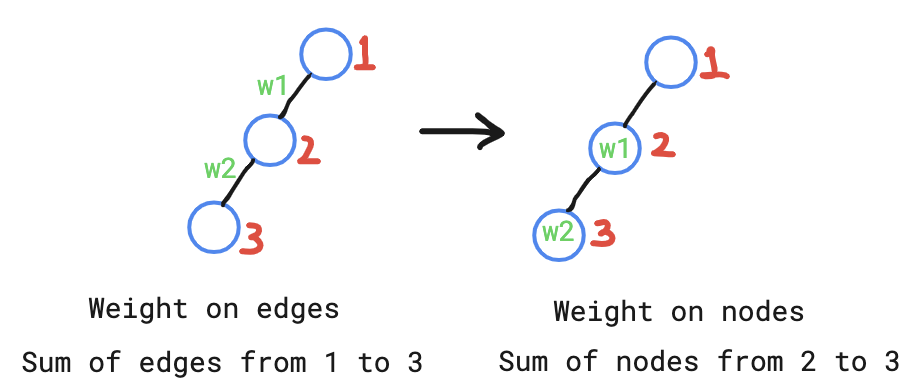
Values stored on Edges

We need to modify the segment tree query based on whether values stored on vertices or edges.

  if (!valuesOnVertices && u == v) return;
  operation(Math.min(pos[u], pos[v]) + (valuesOnVertices ? 0 : 1), Math.max(pos[u], pos[v]));

source: https://sites.google.com/site/indy256/algo/heavy_light

Store the values in the deeper nodes in HLD as update the weight of i-th edge as follows

void update(int i, int w) {
  int u = dep[edges[i].F] > dep[edges[i].S] ? edges[i].F : edges[i].S;
  segtree::update(0, n, pos[u], w);
}

And modify the query as follows, only if u and v are in same chain, then instead of querying from pos[u] to pos[v], we query from pos[v] + 1(the next vertex in this heavy path) to pos[v]. The code needs to be updated as follows.

  int mx = -inf;
  while(head[u] != head[v]) {
    if(dep[head[u]] > dep[head[v]]) swap(u, v);
    mx = max(mx, segtree::query(0, n, pos[head[v]], pos[v]));
    v = fa[head[v]];
  }
  if(dep[u] > dep[v]) swap(u, v);
  if(pos[u] < pos[v]) mx = max(mx, segtree::query(0, n, pos[u] + (valuesOnVertices ? 0 : 1), pos[v]));

SPOJ QTREE

Store the weights of edges in vertices as mentioned above, For update queries: we can update the node value by updating it's position in segment tree.

Solution

const int nax = 1e4 + 5;
 
int ttime = 0;
int sz[nax], top[nax], depth[nax], in[nax], out[nax], par[nax];
vvi Adj;
 
class SegmentTree {                              // OOP style
private:
  int n;                                         // n = (int)A.size()
  vi A, st, lazy;                                // the arrays
 
  int l(int p) { return  p<<1; }                 // go to left child
  int r(int p) { return (p<<1)+1; }              // go to right child
 
  int conquer(int a, int b) {
    if (a == -1) return b;                       // corner case
    if (b == -1) return a;
    return max(a, b);                            // RMQ
  }
 
  void build(int p, int L, int R) {              // O(n)
    if (L == R)
      st[p] = A[L];                              // base case
    else {
      int m = (L+R)/2;
      build(l(p), L  , m);
      build(r(p), m+1, R);
      st[p] = conquer(st[l(p)], st[r(p)]);
    }
  }
 
  void propagate(int p, int L, int R) {
    if (lazy[p] != -1) {                         // has a lazy flag
      st[p] = lazy[p];                           // [L..R] has same value
      if (L != R)                                // not a leaf
        lazy[l(p)] = lazy[r(p)] = lazy[p];       // propagate downwards
      else                                       // L == R, a single index
        A[L] = lazy[p];                          // time to update this
      lazy[p] = -1;                              // erase lazy flag
    }
  }
 
  int RMQ(int p, int L, int R, int i, int j) {   // O(log n)
    propagate(p, L, R);                          // lazy propagation
    if (i > j) return -1;                        // infeasible
    if ((L >= i) && (R <= j)) return st[p];      // found the segment
    int m = (L+R)/2;
    return conquer(RMQ(l(p), L  , m, i          , min(m, j)),
                   RMQ(r(p), m+1, R, max(i, m+1), j        ));
  }
 
  void update(int p, int L, int R, int i, int j, int val) { // O(log n)
    propagate(p, L, R);                          // lazy propagation
    if (i > j) return;
    if ((L >= i) && (R <= j)) {                  // found the segment
      lazy[p] = val;                             // update this
      propagate(p, L, R);                        // lazy propagation
    }
    else {
      int m = (L+R)/2;
      update(l(p), L  , m, i          , min(m, j), val);
      update(r(p), m+1, R, max(i, m+1), j        , val);
      int lsubtree = (lazy[l(p)] != -1) ? lazy[l(p)] : st[l(p)];
      int rsubtree = (lazy[r(p)] != -1) ? lazy[r(p)] : st[r(p)];
      st[p] = conquer(lsubtree, rsubtree);
    }
  }
 
public:
  SegmentTree(int sz) : n(sz), A(n), st(4*n), lazy(4*n, -1) {}
 
  SegmentTree(const vi &initialA) : SegmentTree((int)initialA.size()) {
    A = initialA;
    build(1, 0, n-1);
  }
 
  void update(int i, int j, int val) { update(1, 0, n-1, i, j, val); }
 
  int RMQ(int i, int j) { return RMQ(1, 0, n-1, i, j); }
};
 
 
int dfs(int u, int p){
    sz[u] = 1;
    for(int &v:Adj[u]){
        if(v!=p){
            depth[v] = depth[u] + 1;
            par[v] = u;
            sz[u] += dfs(v, u);
            if(sz[v] > sz[Adj[u][0]])
                swap(Adj[u][0], v);
        }
    }
    return sz[u];
}
 
void hld(int u, int p){
    in[u] = ttime++;
    for(int v:Adj[u]){
        if(v == p) continue;
        top[v] = (v == Adj[u][0] ? top[u] : v);
        hld(v, u);
    }
    out[u] = ttime;
}
 
struct Edge{
    int a, b, w;
    Edge(int _a, int _b, int _w) : a(_a), b(_b), w(_w) {}
};
 
void solve(){
    int n;
    scanf("%d", &n);
 
    Adj = vvi(n, vi());
    vector<Edge> E;
    for(int i=0;i<n-1;i++){
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);
        a--;b--;
        Adj[a].push_back(b);
        Adj[b].push_back(a);
        Edge e(a,b,w);
        E.push_back(e);
    }
 
    depth[0] = 0;
    par[0] = 0;
    ttime = 0;
    dfs(0, -1);
    hld(0, -1);
    SegmentTree st(n);
    for(Edge e:E){
        if(depth[e.a] < depth[e.b])
            swap(e.a, e.b);
        st.update(in[e.a], in[e.a], e.w); // update deeper node
    }
 
    while(true){
        char s[40];
        scanf("%s", s);
        if(s[0] == 'D') break;
        if(s[0] == 'C'){
            int i, ti;
            scanf("%d %d", &i, &ti);
            i--;
            Edge e = E[i];
            if(depth[e.a] < depth[e.b])
                swap(e.a, e.b);
            st.update(in[e.a], in[e.a], ti); // update deeper node
        }else{
            int u, v;
            scanf("%d %d", &u, &v);
            u--; v--;
            int res = 0;
            while(true){
                int x = top[u], y = top[v];
                if(x == y){
                    if(depth[u]>depth[v]) swap(u,v); // u is top
                    res = max(res, st.RMQ(in[u]+1, in[v]));
                    break;
                }
                if(depth[x] > depth[y]){
                    // query from x to u
                    res = max(res, st.RMQ(in[x], in[u]));
                    u = par[x];
                }else{
                    // query from y to v
                    res = max(res, st.RMQ(in[y], in[v]));
                    v = par[y];
                }
            }
            printf("%d\n", res);
        }
    }
}
 
int main(){
    int TC;
    scanf("%d", &TC);
    while(TC--){
        solve();
    }
    return 0;
}

SPOJ QTREE2

You are given a tree (an undirected acyclic connected graph) with N nodes, and edges numbered 1, 2, 3...N-1. Each edge has an integer value assigned to it, representing its length.

We will ask you to perfrom some instructions of the following form:

• DIST a b : ask for the distance between node a and node b
• KTH a b k : ask for the k-th node on the path from node a to node b

Solution We can answer distance queries in similar way as QTREE by storing edge weights in the deeper node and doing sum query.

To answer KTH a b k, we will check whether k-th node from a is on 1) the path from a to lca(a,b) or 2) the path from lca(a,b) to b. To find this we can use dist[a, lca(a,b)] = depth[a] - depth[lca(a,b)], once we know on which vertical path it lies we can do move between heavy-chains and find the k-th in log n time. This is similar to binary lifting algorithm.

SPOJ QTREE3

You are given a tree (an acyclic undirected connected graph) with N nodes. The tree nodes are numbered from 1 to N. In the start, the color of any node in the tree is white.

We will ask you to perfrom some instructions of the following form:

• 0 i : change the color of the i-th node (from white to black, or from black to white); or
• 1 v : ask for the id of the first black node on the path from node 1 to node v. if it doesn't exist, you may return -1 as its result.

Solution: To answer type 2 queries fastly, we will need to go through path from v to 1 querying the topmost black node in each heavy path. In the following solution, instead of segment tree, we have used set<pair<height[node], node>> to store the black nodes seperately for each heavy chain. This way we can find the topmost black node in heavy chain in O(1) time, so the total time for queries of the form 1 v is O(log n). Only important thing is consider the node above node v by checking the height of nodes in query(This if(depth[temp] <= depth[u]) ans = temp; in code takes care of this).

Queries of the form 0 i can also be done in O(log n) time by adding(if node color is changed from white to black) the node to set or removing(if node color changes from black to white) the node from the set of this heavy chain.

CPP solution using set instead of Segment tree

const int nax = 100005;

int n, nchain;
int chain[nax], par[nax], sz[nax], depth[nax], top[nax];
set<pair<int,int>> st[nax]; // pair(height, node) of black nodes in this chain

vvi Adj;

int dfs(int u, int p){
    sz[u] = 1;
    par[u] = p;
    for(int &v:Adj[u]){
        if(v==p) continue;
        depth[v] = depth[u] + 1;
        sz[u] += dfs(v, u);
        if(sz[v] > sz[Adj[u][0]])
            swap(v, Adj[u][0]);
    }
    return sz[u];
}

void hld(int u, int p){
    chain[u] = nchain;
    for(int v:Adj[u]){
        if(v == p) continue;
        top[v] = (v == Adj[u][0] ? top[u] : v);
        if(v != Adj[u][0]) nchain++;
        hld(v, u);
    }
}

void update(int u){
    pair<int, int> X = {depth[u], u};
    if(st[chain[u]].count(X)) // if node color changes from black to white
        st[chain[u]].erase(X);
    else st[chain[u]].insert(X);
}

int query(int u){
    int ans = -1;
    while(u != -1){
        if(st[chain[u]].size() > 0){
            int temp = st[chain[u]].begin() -> second;
            // If u and temp belong in same chain
            // consider nodes above u only
            if(depth[temp] <= depth[u]) ans = temp;
        }
        u = par[top[u]];
    }
    return ans;
}

int main(){
    int q;
    scanf("%d%d", &n, &q);
    Adj = vvi(n, vi());
    for(int i=0;i<n-1;i++){
        int a, b;
        scanf("%d%d", &a, &b);
        a--;b--;
        Adj[a].push_back(b);
        Adj[b].push_back(a);
    }
    dfs(0, -1);
    hld(0, -1);
    while(q--){
        int type, node;
        scanf("%d %d", &type, &node);
        node--;
        if(type == 0){
            update(node);
        }else{
            int ans = query(node);
            if(ans == -1) printf("%d\n", ans);
            else printf("%d\n", ans + 1);
        }
    }
    return 0;
}

We can also solve this problem by using Segment tree by storing {height[i], i} in each black node and using minimum to combine nodes for building the tree. In this case we will need to make height[i] = INF in case the node is white color.

Another way to solve this problem is to use true or false based on the color of nodes in each tree node return node value in case it is true. Use 0 for white color and 1 for black color.

Segment tree should answer the following: index of left most black node in a range.

Solution using Segment Tree

void update(int node, int l, int r, int i, int val){
    if(l>i || r<i) return;
    if(l==r){
    	tree[node]^=val;
	return;
    }
    int mid = (l+r)/2;
    update(node*2, l, mid, i, val);
    update(node*2+1, mid+1, r, i, val);
    tree[node] = tree[node*2] | tree[node*2+1];
}

int query(int node, int tl, int tr, int l, int r){
    if(tl>r || tr<l) return -1;
    if(tree[node]==false) return -1; // no black node
    if(tl==tr) return node_at_pos[tl];
    int mid = (tl+tr)/2;
    int d = query(node*2, tl, mid, l, r);
    // d == -1 => no black node in left subtree (tl, mid)
    if(d == -1) return query(node*2+1, mid+1, tr, l, r);
    return d;
}

// While building hld, we should store node_at_pos[i] along with pos[node]

We can even speed up the above solution by storing the value of left most index whose color is black.

SPOJ QTREE6

TODO: https://discuss.codechef.com/t/qtree6-editorial/3906 & https://www.codechef.com/viewsolution/3054419 & https://www.codechef.com/viewsolution/3050051

Non - recursive implementation https://codeforces.com/blog/entry/67149

Problem can be solved by both HLD and Centroid Tree: https://codeforces.com/blog/entry/67388 https://codeforces.com/contest/1174/problem/F

REF

• https://blog.anudeep2011.com/heavy-light-decomposition/
• https://codeforces.com/blog/entry/81317
• https://codeforces.com/blog/entry/22072
• https://codeforces.com/blog/entry/12239
• https://apps.topcoder.com/forums/?module=Thread&threadID=796128&start=0&mc=8