Notes

F. Chests and Keys

source: https://codeforces.com/contest/1519/problem/F

Solution:

Clearly, if the sum of the coins in all the chests > cost of buying all the keys, then Bob always gains positive profit and answer is -1.

Observation: Note that here n, m, aᵢ and bⱼ are small. Bob's profit should be strictly positive > 0.

Firstly, let's try to find some naive solution for this problem. Let's iterate on the subset of locks Alice puts on the chests. After choosing the subset of locks, how to check whether Bob can gain positive profit? We can iterate on the subset of keys he can buy as well, but in fact, this problem has a polynomial solution.

Brute force solution is to iterate over each pair of (chest, lock) and decide whether we have to put this lock on the chest or not. We have mn = 36 number of pairs, So 2^36 will time out.

Constriants are small, can we use dp? We will need to store a lot of information in each state.

We have to minimise the cost paid by Alice, Let's say Alice has picked his locks, what will Bob do? how about modelling as as flow problem? Motivation for this is Project and tools problem. Source: Neal

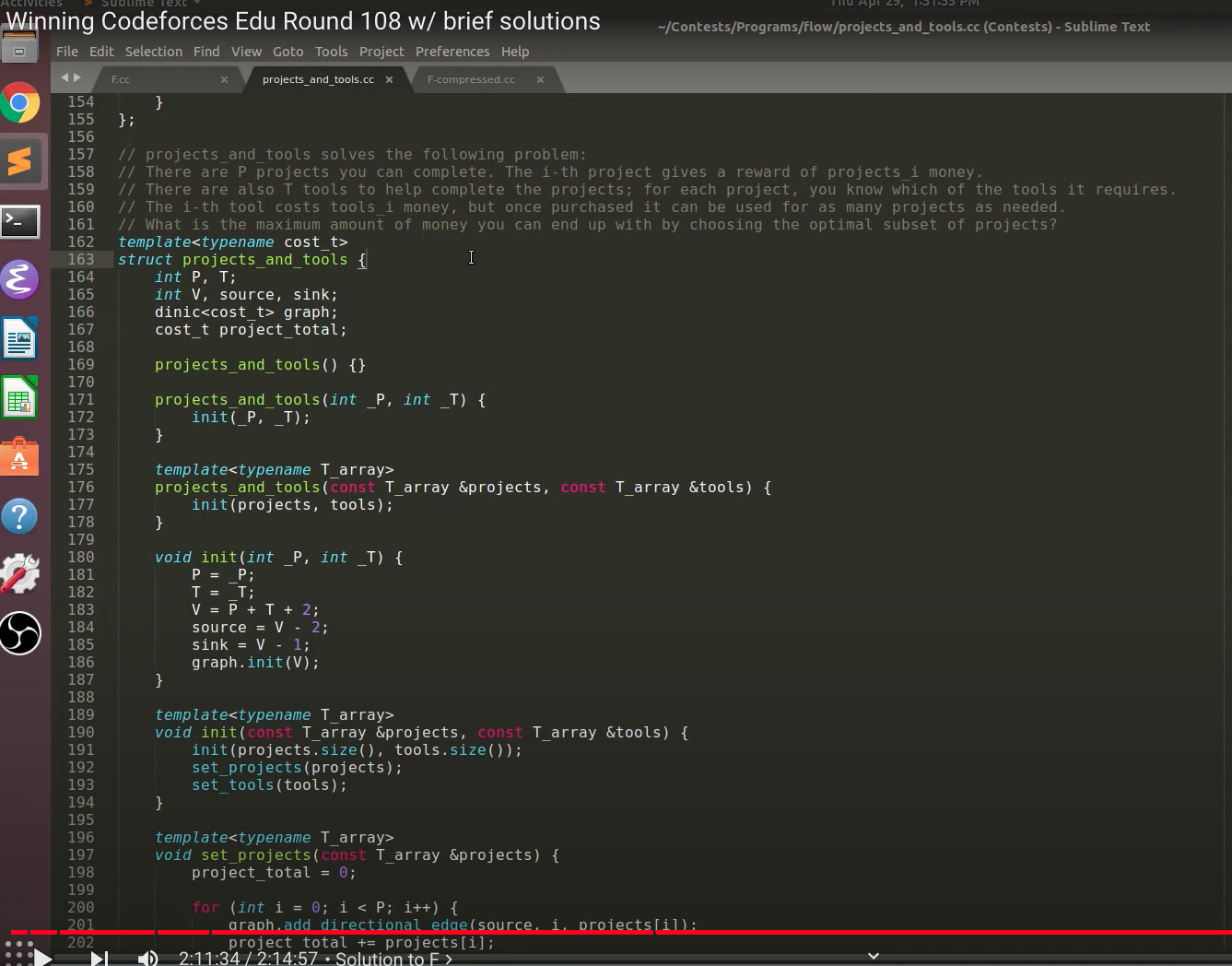
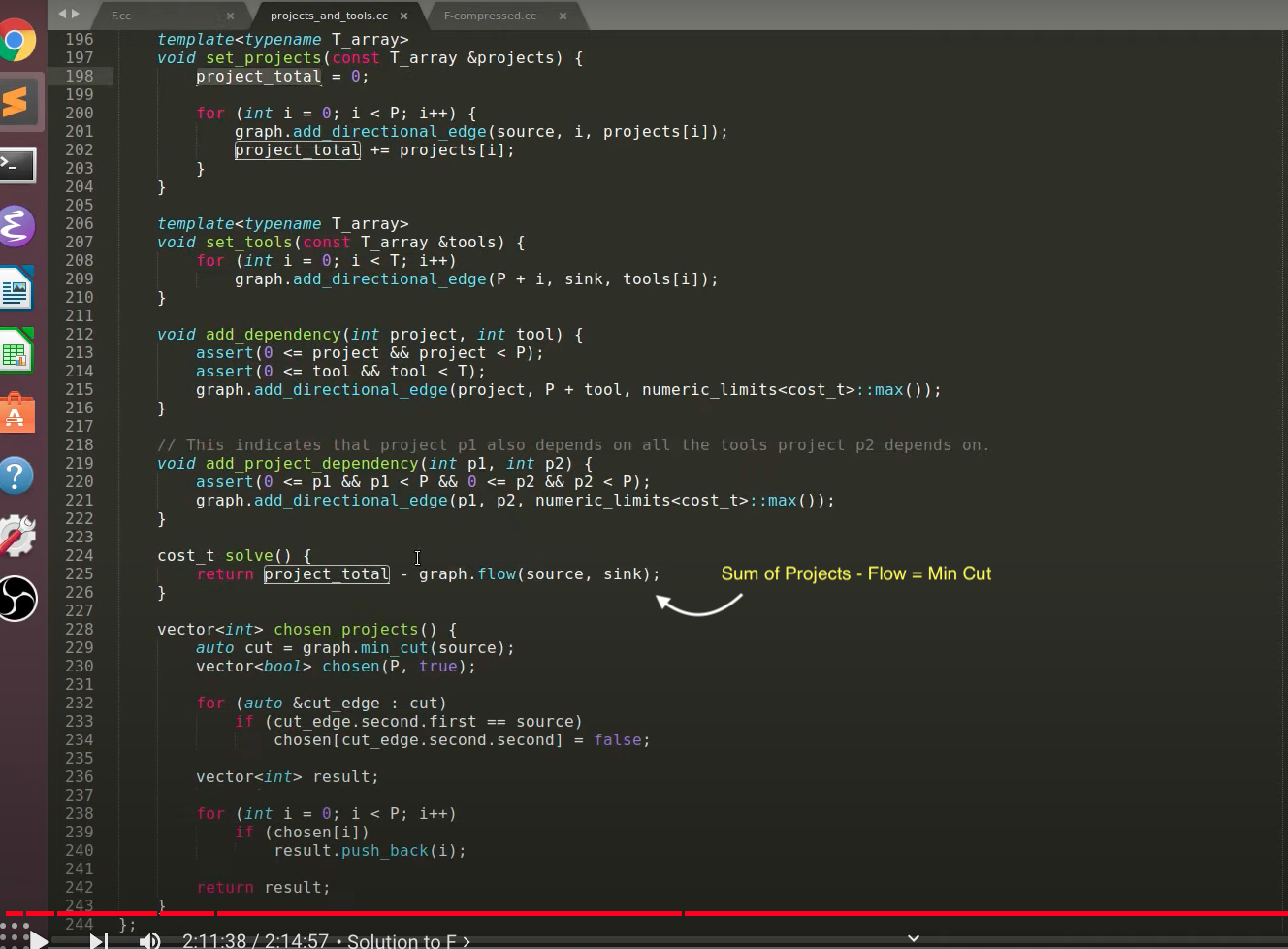
Here basically, chests are projects and keys are tools.

Suppose that we have decided the subset of pairs {chests, locks} that Alice has decided, then:

Consider the flow network as follows:

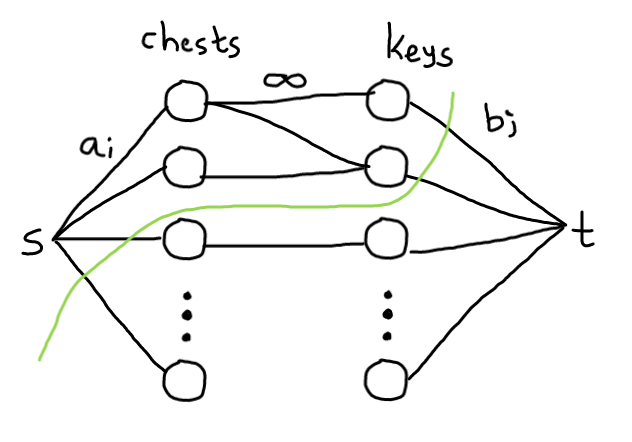
If we find the minimum cut from the source to the sink, then Bob's profit is sum(aᵢ) - min_cut.

Key idea

Unfortunately, even iterating through all subsets of locks is too slow. To improve this solution, we should look at the minimum cut and its usage a bit more in detail. Notice that Bob can always take no keys and open no chests to get a profit of zero, so Alice's goal is to ensure that it is the best Bob's option. If Bob takes no chests and no keys, it means that the cut divides the network into two parts: the source and all other vertices. And, in terms of flows, it means that the maximum flow in this network should saturate all arcs going from the source (I highlighted it because it is the key idea of the solution).

If Alice has to win, we need to make sure that Bob will not be able to make positive profit, in other words, project_total - min_cost = 0 that is project_total = maximum_flow. So essentially, we will need to choose minimum cost pairs {chests, locks} that is c_ij which saturates the edges outgoing from s, thus disconnecting s from other nodes in the graph.

Problem boils down to

We have 6 nodes on the chests of the graph, each node can store flow from 0 to 4, so we have 5^6 states for flow. We can find what is the minimum cost required for the prefix on the left to maintain this flow, to do this we can go through one by one node for each of the keys nodes and use dynamic programming.

Here the constraints on a𝑖, n and m come in handy. We can use a dynamic programming with the flow over all arcs going from the source as one of the states. One of the ways to implement it is to have (f₁, f₂ ,…, fₙ , i, j, r) as the state, where f₁ through fₙ are the values of the flow going from the arcs from the source, i is the current vertex in the left part we consider,j is the current vertex in the right part we consider, and r is the flow we already pushed through the arc connecting vertex j of the right part to the sink (and the value we store for this state is the minimum cost Alice has pay to reach this state).

There are two basic types of transitions in this dynamic programming: we either skip the arc from i to j, or pick it and transfer some flow through it; and no matter what we've chosen, we move to the next vertex of the left part (or to 1 and increase j by 1 if we are already considering the n-th vertex of the left part). The constraints were loose enough to implement this dp basically in any form (there was no need to compress the states into single integers).

Maximum weight Matching problem

Problem

There are N competitive programmers.

Consider a team consisting of some of the N people. Let us call such a team a dream team if both of the following conditions are satisfied:

Let k be the maximum possible number of members of a dream team. For each i=1,2,…,k, solve the following question. Question: find the maximum sum of power of people belonging to a dream team consisting of i people.

Solution