Notes

• Given is a trial that succeeds in probability p ( p ≠ 0 ) . Then the expected number of trials until the first success (including the last succeeding one) is 1/p .

Proof: Let X be the desired expected value. After a trial, we can terminate the trials if it is successful, while we go back to the starting point if unsuccessful; therefore we have equation X = 1 + ( 1 − p ) X . By transformation we have p X = 1 , thus X = 1/p .

Tree Array

You are given a tree consisting of n(2≤ n ≤ 200) nodes. You generate an array from the tree by marking nodes one by one.

Initially, when no nodes are marked, a node is equiprobably chosen and marked from the entire tree.

After that, until all nodes are marked, a node is equiprobably chosen and marked from the set of unmarked nodes with at least one edge to a marked node.

The final array 𝑎 is the list of the nodes' labels in order of the time each node was marked. Find the expected number of inversions in the array that is generated by the tree and the aforementioned process.

source: https://codeforces.com/contest/1540/problem/B

Solution:

Fix the initial node chosen and root the tree there, what is the contribution of each pair of nodes? Say we have two nodes a and b and value at a < b now a inversion pair (a, b) is counted only if b is choosen before a. Nothing matters besides the path from node a to node b, and the initially chosen node c.

Suppose we start by marking the root. To mark a or b, we must first mark the lca, so we may assume that the lca has just been marked. Before marking the lca, there is no way to make more progress towards 𝑏 than 𝑎 or vice versa.

Fixing a given root c, the expected value of the entire process is obviously the sum of the expected values for a fixed root divided by n.

Find the contribution of the inversion of two nodes (a,b) where a < b. The expected contribution for any pair (a,b) is equal to the probability that b appears before a with a given root.

It depends on the probabilty from distance of lca(a,b) and a and the distance of lca(a,b) and b. Suppose that F[x][y] defines the probability that node b is visited first than node a, then 𝐹[𝑥][𝑦] = (𝐹[𝑥−1][𝑦] + 𝐹[𝑥][𝑦−1])/2. Intuitively, this is because the probability of decreasing x or decreasingy is always the same, so the probability of transitioning the state we end up transitioning to is always the same.

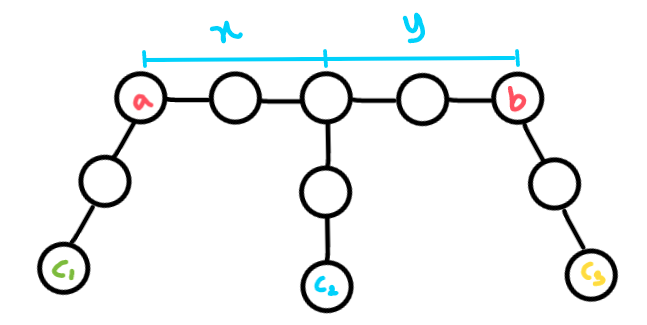
For any node c₂ which is in between a and b, x = dist[a][c₂] - d where d = (dist[a][c₂] + dist[b][c₂] - dist[a][b])/2, d is the distance from c₂ to lca(a, b) when tree is rooted at c₂. For any node c₁ → x = 0 and for any node c₃ → y = 0.

#include<bits/stdc++.h>

using namespace std;

# define ll long long

int MOD = 1e9 + 7;

struct mi {
 	int v; explicit operator int() const { return v; } 
	mi() { v = 0; }
	mi(ll _v):v(_v%MOD) { v += (v<0)*MOD; }
};
mi& operator+=(mi& a, mi b) { 
	if ((a.v += b.v) >= MOD) a.v -= MOD; 
	return a; }
mi& operator-=(mi& a, mi b) { 
	if ((a.v -= b.v) < 0) a.v += MOD; 
	return a; }
mi operator+(mi a, mi b) { return a += b; }
mi operator-(mi a, mi b) { return a -= b; }
mi operator*(mi a, mi b) { return mi((ll)a.v*b.v); }
mi& operator*=(mi& a, mi b) { return a = a*b; }
mi pow(mi a, ll p) { assert(p >= 0); // asserts are important! 
	return p==0?1:pow(a*a,p/2)*(p&1?a:1); }
mi inv(mi a) { assert(a.v != 0); return pow(a,MOD-2); }
mi operator/(mi a, mi b) { return a*inv(b); }


const int inf = (int)1e8;
const int nax = 205;

mi F[nax][nax];

int main() {
    int n;
    scanf("%d", &n);
    vector<vector<int>> G(n, vector<int>(n, inf));
    for(int i=0;i<n-1;i++){
        int x, y;
        scanf("%d %d", &x, &y);
        x--; y--;
        G[x][y] = 1; G[y][x] = 1;
    }

    // floyd warshall - all pairs shortest path
    for(int k=0;k<n;k++)
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                G[i][j] = min(G[i][j], G[i][k] + G[k][j]);


    // calculate probabilities based on distance x, y
    F[0][0] = 0;
    for(int i=1;i<n;i++){
        F[0][i] = 0;
        F[i][0] = 1;
    }
    for(int i=1;i<n;i++)
        for(int j=1;j<n;j++)
            F[i][j] = (F[i-1][j] + F[i][j-1])/2;


    mi ans = 0;
    for(int a=0;a<n;a++){
        for(int b=a+1;b<n;b++){
            for(int c=0;c<n;c++){
                int x = G[a][c], y = G[b][c];
                int d = (x + y - G[a][b])/2;
                x -= d; y -= d;
                ans += F[x][y];
            }
        }
    }
    printf("%d\n", (int)(ans/n));
    return 0;
}

source: tourist https://codeforces.com/contest/1540/submission/120542169

Maximum of n Dice Roll

Find expected value of maximum of n dice roll. First find the probability that maximum of n dice roll is x

source: https://codeforces.com/problemset/problem/453/A

Follow up: https://math.stackexchange.com/questions/1696623/what-is-the-expected-value-of-the-largest-of-the-three-dice-rolls

Lottery

Each time he takes a draw, he gets one of the N prizes available. What is the probability that he gets exactly M(1 ≤ M ≤ N ≤ 50) different prizes from K(1 ≤ K ≤ 50) draws.

Ref: https://atcoder.jp/contests/abc243/tasks/abc243_f

#include<bits/stdc++.h>
#include<atcoder/all>
using namespace std;
using namespace atcoder;
using mint = modint998244353;

mint dp[51][51][51];
int w[51];
mint p[51];
mint fact[51];
int main(){
	int n,m,k;
	cin >> n >> m >> k;
	
	for(int i=0;i<n;i++)cin >> w[i];
	mint wsum=0;
	for(int i=0;i<n;i++)wsum+=w[i];
	for(int i=0;i<n;i++)p[i]=w[i]/wsum;
	
	fact[0]=1;
	for(int i=1;i<=50;i++)fact[i]=fact[i-1]*i;
	
	dp[0][0][0]=1;
	for(int x=0;x<n;x++)for(int y=0;y<=m;y++)for(int z=0;z<=k;z++){
		for(int c=0;c<=k-z;c++){
			dp[x+1][y+(c!=0)][z+c]+=dp[x][y][z]/fact[c]*p[x].pow(c);
		}
	}
	cout << (dp[n][m][k]*fact[k]).val() << endl;
}

Indicator variables to solve expected values

Ref: https://www.cs.princeton.edu/courses/archive/fall06/cos341/handouts/variance-notes.pdf

Also, check this problem: https://www.hackerearth.com/problem/algorithm/blocked-matrix-ce17659d/?purpose=login&source=problem-page&update=google